Les mesures de dispersion
Pour illustrer les mesures de dispersion, prenons pour exemple un échantillon de 9 morues de l'Atlantique (Gadus morhua).

Pour cet échantillon de 9 morues, nous allons étudier la dispersion de la taille de ces poissons en calculant les paramètres suivants :
Pour commencer, mesurons la taille de ces 9 poissons, ainsi que la moyenne de ces tailles, qui vaut ici 65 cm :
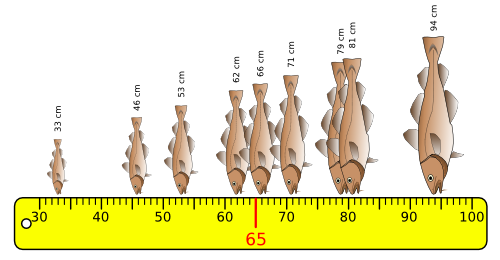
L'amplitude :
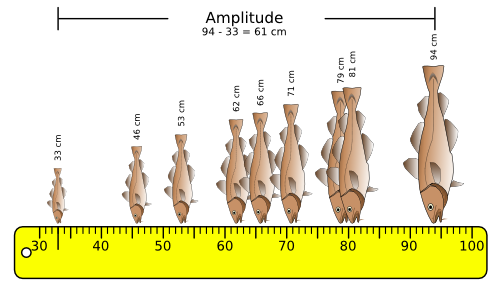
Définition : L'amplitude (ou étendue) d'un échantillon est l'écart qui sépare la valeur la plus petite de la valeur la plus grande.
Formule : amplitude = valeur maximale - valeur minimale
Domaine : L'amplitude peut prendre des valeurs qui vont de 0 à l'infini.
La variance :
Définition : La variance est le reflet numérique de la dispersion des valeurs autour de la moyenne.
Elle est obtenue à partir des écarts des valeurs par rapport à la moyenne.
Ecarts à la moyenne :
Pour chaque valeur on calcule l'écart qui le sépare de sa moyenne arithmétique : TeX Embedding failed!
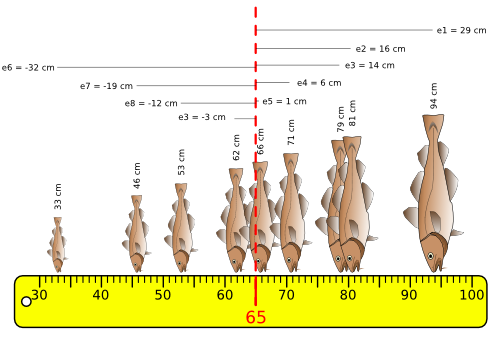
La somme de ces écarts est nulle. Elle ne peut donc être utilisée comme un estimateur mathématique de la dispersion des valeurs.
Carrés des Ecarts à la moyenne :
Pour chacun des écarts précédents, on calcule son carré. Ainsi pour chaque valeur on obtient une valeur positive, et leur somme n'est jamais nulle, sauf si les écarts sont nuls (valeurs égales à la moyenne).
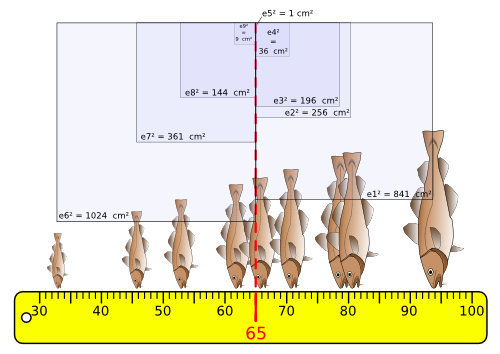
Si on additionne tous ces carrés d'écarts :
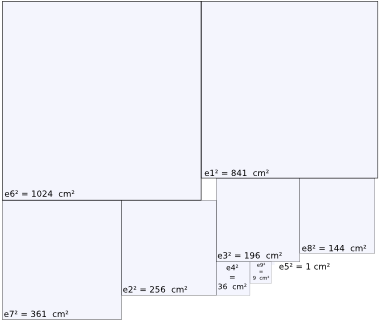
Cela donne :

La somme des carrés des écarts (SCE) sera d'autant plus grande que les valeurs seront éloignées de la moyenne. C'est donc un bon estimateur de la dispersion des valeurs autour de la moyenne.
| TeX Embedding failed! |
Cependant, à dispersion équivalente, la SCE sera toujours d'autant plus grande qu'il y aura un nombre important de valeurs. Pour que le paramètre de dispersion soit indépendant du nombre de valeurs, on calcule le carré moyen ou la variance.
Carré moyen ou variance :
Le carré moyen ou variance représente la surface moyenne des carrés d'écarts. C'est la SCE/n.
Elle caractérise la distribution des valeurs autour de la moyenne.
Elle est exprimée dans le carré des unités des valeurs, ici en cm2.
Formule : Elle se calcule en sommant les carrés des écarts (SCE = Somme de Carrés des Écarts), et en divisant cette somme par le nombre de valeurs.
| TeX Embedding failed! |
Domaine : La variance est comprise entre 0 et l'infini.
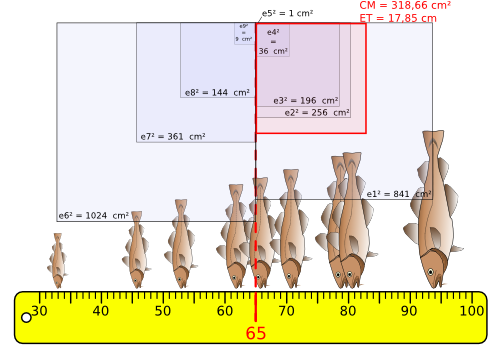
A partir des données numériques d'un échantillon, il est aussi possible d'estimer la variance de la population d'où provient cet échantillon. Dans ce cas, la somme des carrés des écarts est divisée par n-1 et non par n. Quand le nombre d'observations est élevé, la division par n-1 ou par n n' a plus beaucoup d'importance.
| TeX Embedding failed! |
L'écart-type :
La variance étant exprimée dans le carré des unités, on lui préfère souvent l'écart-type, ou racine carrée de la variance. L'écart-type a les mêmes unités que les données et que la moyenne.
Définition : L'écart-type représente l'écart quadratique moyen des valeurs par rapport à la moyenne.
Formule : L'écart-type (ET ou S) est la longueur du côté du carré moyen. Selon que l'on veut simplement décrire l'ensemble des données ou estimer l'écart-type de la population d'origine, on utilisera la racine carrée de la variance SCE/n ou SCE/(n-1)
| TeX Embedding failed! |
Domaine : L'écart-type est compris entre 0 et l'infini.
Le coefficient de variation :
Définition : Le coefficient de variation représente le rapport de l'écart-type par la moyenne.
Formule :
| TeX Embedding failed! |
Domaine : Le coefficient de variation est compris entre 0 et l'infini.
Utilisation : Le CV est indépendant des unités de mesure. Il permet de comparer la dispersion de données exprimées dans des unités de mesure différentes (par exemple, poids exprimé en kg ou en gr). Il est également utilisé pour comparer la dispersion des mesures quelle que soit la valeur de la moyenne.
- Version imprimable
- Vous devez vous identifier ou créer un compte pour écrire des commentaires