Les tests d'hypothèses permettent de comparer des populations entre elles au moyen d'échantillons ou encore de comparer un échantillon avec une population de référence...

Types de tests d'hypothèses

Les tests d'hypothèses permettent de comparer des populations entre elles au moyen d'échantillons ou encore de comparer un échantillon avec une population de référence...

Dans le cadre de ces travaux pratiques, nous envisagerons trois types de tests d'hypothèses :

1. test de comparaison d'une moyenne à un standard (1 échantillon)
2. test de comparaison de 2 moyennes : 2 échantillons indépendants
3. test de comparaison de 2 moyennes : 2 échantillons non indépendants ou observations pairées

Les tests 2 et 3 peuvent être également traités par l'ANOVA.

Les hypothèses

Quel que soit le type de tests (voir ci-dessus), on formule l'hypothèse de référence que les moyennes comparées proviennent d'une seule population de moyenne µ. Il s'agit de l'hypothèse de départ appelée "hypothèse nulle" (H0) qui pourra s'écrire comme suit dans le cas d'une comparaison de deux moyennes:

TeX Embedding failed!

Le contraire de l'hypothèse nulle est qu'une des populations possède une moyenne plus grande, plus petite ou tout simplement différente par rapport à l'autre population. Il s'agit de l'"hypothèse alternative" (H1) qui pourra s'écrire comme suit:

TeX Embedding failed!
ou TeX Embedding failed!
ou encore TeX Embedding failed!

 Les statistiques aident l'expérimentateur à choisir entre l'hypothèse nulle et l'hypothèse alternative

Réalisation du test

Réduction des moyennes observées:
En considérant l'hyptohèse nulle vraie, la (les) moyenne(s) mx obtenue(s) pour (les) l'échantillon(s) peu(ven)t être réduite(s) en une valeur observée (z observée ou t observée). Celle-ci peut ensuite être comparée à une valeur seuil (z table ou t table).

Recherche d'une limite arbitraire, une valeur seuil:

La valeur seuil va déterminer sous la courbe de Gauss réduite des zones distinctes: une zone probable suivant H0 et une zone peu probable suivant H0. Cette valeur seuil est déterminée par la valeur de alpha, choisie arbitrairement à 5%, 1% ou 0,1%. Le alpha choisi détermine donc une zone de valeurs de z ou de t peu probables sous H0.

Comparer la valeur réduite observée à la valeur seuil trouvée dans les tables:

Si l'hypothèse alternative H1 est " µ2 plus grand que  µ1"

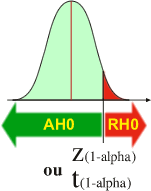
Lorsque la valeur observée (Z observée ou t observée) est plus grande que la valeur seuil (Z_(1-alpha) ou t_(1-alpha)), l'H0 est rejetée. La valeur observée est trop différente de la valeur attendue sous H0 pour considérer qu'elle est due au hasard de l'échantillonnage.

Dans le cas d'un rejet de H0 (RH0), l'expérimentateur aura réussi à démontrer que les moyennes observées sont telles que µ2 est vraisemblablement plus grande que  µ1. Comme la valeur de alpha choisie par l'expérimentateur est faible (maximum 5%), un RH0 signifie que la distance qui sépare les moyennes comparées est trop grande pour être simplement due au hasard. Le risque de se tromper lorsqu'on rejette RH0 est au maximum égal à alpha et si la valeur de z ou de t est très éloignée de la valeur seuil , la probabilité de se tromper est de loin inférieure à alpha. Dans ce cas, l'expérimentateur est quasiment "certain" que µ2 est bien plus grand que µ1.

Dans le cas d'une acceptation de H0 (AH0), rien ne permet à l'expérimentateur de dire que les moyennes sont différentes. Cette AH0 doit être considérée par l'expérimentateur comme une expérience non interprétable ou "non significative". A la différence de la "quasi certitude" au sujet de la conclusion tirée quand RH0, dans le cas d'une AH0, rien ne permet à l'expérimentateur d'être certain que les moyennes comparées sont effectivement identiques.

Si l'hypothèse alternative H1 est " µ2 plus petit que  µ1"

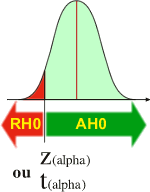
Lorsque la valeur observée (Z observée ou t observée) est plus petite que la valeur théorique (Z_(alpha) ou t_(alpha)), alors H0 est rejetée (RH0).

Dans le cas d'un rejet de H0 (RH0), l'expérimentateur peut affirmer que  µ2 est plus petit que  µ1 avec une probabilité de se tromper de alpha (maximum 5%).

Dans le cas d'une acceptation de H0 (AH0), l'expérimentateur n'a pas réussi à démontrer que  µ2 est plus petite que  µ1. La différence observée entre les moyennes d'échantillon pourrait s'expliquer par le jeu aléatoire de l'échantillonnage.

Si l'hypothèse alternative H1 est " µ2 différent de  µ1"

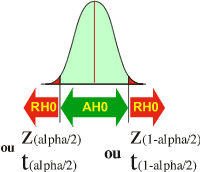
Lorsque la valeur observée (Z observée ou t observée) est SOIT plus petite que la valeur théorique (Z_(alpha/2) ou t_(alpha/2)), SOIT plus grande que la valeur théorique (Z(_1-alpha/2) ou t_(1-alpha/2)), alors H0 est rejetée (RH0).

Dans le cas d'un rejet de H0 (RH0), l'expérimentateur peut affirmer que µ2 est différent de µ1 avec une probabilité de se tromper de alpha (maximum 5%).

Dans le cas d'une acceptation de H0 (AH0), l'expérimentateur n'a pas réussi à démontrer que  µ2 est différent de µ1. La différence observée entre les moyennes d'échantillon pourrait s'expliquer par le jeu aléatoire de l'échantillonnage.