1. Savoir d'où l'on part et ce qu'on souhaite démontrer

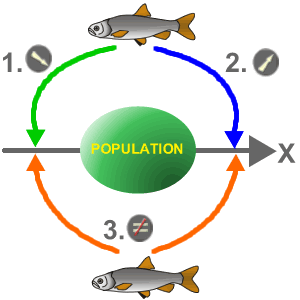
Un expérimentateur a mesuré un chevaine de 3 ans et veut le comparer à la population de chevaines de 3 ans centrée sur µ. Son point de départ est de dire que l'individu est conforme à cette population: c'est l'hypothèse nulle H0. Ce qu'il veut démontrer est SOIT:

1. que le poisson mesuré est plus petit que prédit par la normale et appartient à une population centrée sur µ1 plus petite que µ (en vert)
   Dans ce cas, on peut poser les hypothèses suivantes: H0: µ = µ1 et H1: µ1 inférieure à µ. Il s'agira alors d'un test unidirectionnel à gauche.
2. que le poisson mesuré est plus grand que prédit par la normale et appartient à une population centrée sur µ1 plus grande que µ (en bleu)
   Dans ce cas, on peut poser les hypothèses suivantes: H0: µ = µ1 et H1: µ1 supérieure à µ. Il s'agira alors d'un test unidirectionnel à droite.
3. que le poisson mesuré est ou plus grand ou plus petit (différent) que prédit par le modèle et appartient à une population centrée sur µ1 plus grande OU plus petite que µ (en orange)
   Dans ce cas, on peut poser les hypothèses suivantes: H0: µ = µ1 et H1: µ1 différente de µ. Il s'agira alors d'un test bidirectionnel.

Le choix de l'hypothèse alternative H1 se fait en fonction des connaissances a-priori ou scientifiques de l'expérimentateur (par exemple, conditions d'élevage favorables ou défavorables) et NON en fonction de la valeur observée qui peut être inférieure ou supérieure à la valeur attendue simplement par le jeu de l'échantillonnage aléatoire.

2. Convertir la valeur observée en une valeur réduite

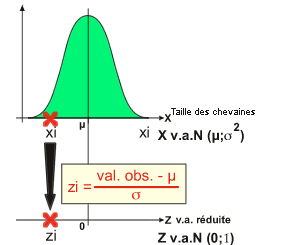
L'expérimentateur a obtenu une taille pour le poisson capturé (ou une taille moyenne s'il en a capturé plusieurs). Pour faciliter sa prise de décision (Accepter le fait que ce poisson est normal [acceptation de H0 = AH0] ou non [rejet de H0 = RH0]), il va réduire la valeur observée en une valeur réduite (z réduit, t réduit, ...).

3. Rechercher dans les tables réduites correspondantes la ou les valeurs seuil:

En fonction du alpha déterminé par l'expérimentateur et de l'hypothèse H1 choisie, il va définir un seuil de signification particulier.

1. Test unidirectionnel à gauche: Z_α
2. Test unidirectionnel à droite: Z_1-α
3. Test bidirectionnel: TeX Embedding failed! ou TeX Embedding failed!

Exemple

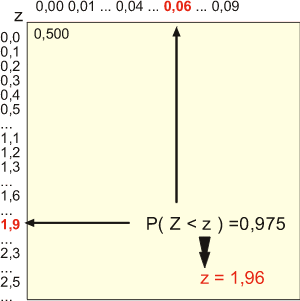
Soit une différence à mettre en évidence pour un alpha de 5% (test bidirectionnel: il y a donc 2 seuils à trouver Z_0,025 et z_0,975) .

Dans la table, on localise la valeur la plus proche de 0,975 afin de trouver z_0,975. Le z trouvé dans les tables est de 1,96. Par symétrie, on peut déduire le z_0,025: -1,96

Conclusion du test

En comparant la valeur réduite des observations (z observé) avec la valeur seuil trouvée dans les tables, l'expérimentateur peut tirer une conclusion à son test.

Exemple

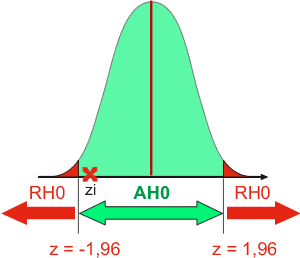
Soit une valeur de z observée de -1,84 pour un test bidirectionnel avec un alpha de 5%. Dans ce cas, -1,84 est compris entre -1,96 et 1,96. La valeur étant comprise entre les deux valeurs seuils, elle est considérée comme "normale". Cela revient à dire que la probabilité d'obtenir une valeur (1,84) aussi éloignée de 0 est plus grande que 5%. On considère donc que l'événement est probable sous H0 et que la valeur observée est due au hasard de l'échantillonnage.

La conclusion au test est la suivante: La différence entre la mesure observée et la valeur attendue peut être attribuée au hasard de l'échantillonnage. Par conséquent, on accepte l'hypothèse nulle (AH0).

Si la valeur observée n'était pas comprise entre -1,96 et 1,96, l'expérimentateur aurait pu conclure que la mesure observée était trop différente de la normale ou trop peu probable sous H0 (< 5%). Par conséquent,  il aurait rejeté l'hypothèse nulle (RH0).

Remarque

Dans le cas d'un test bidirectionnel, RH0 signifie bien sûr la mise en évidence d'une différence de la valeur observée par rapport à la normale MAIS on peut aller plus loin. En effet, pour un même alpha MAIS pour un test unidirectionnel, on aura aussi un RH0. L'expérimentateur pourra donc dire qu'il y a une différence de la mesure mais aussi que celle-ci est plus grande ou plus petite que la normale.

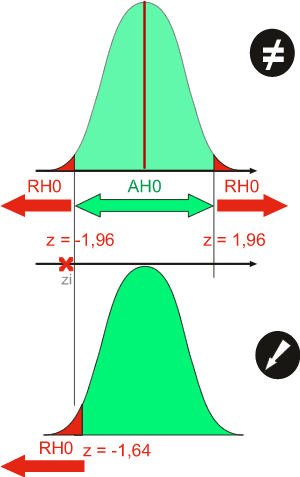
Attention: La conclusion inverse n'est pas vraie. Ce n'est pas parce qu'on rejette l'hypothèse nulle (RH0) dans un test unidirectionnel avec un alpha déterminé qu'il y a rejet de l'hypothèse nulle (RH0) pour un test bidirectionnel avec le même alpha.