Tests d'hypothèses simples relatifs aux moyennes

Outils pédagogiques complémentaires
Exercices en tableurs: 
Acclimation du blaireau
Acidité du raisin
Cotes d'étudiants
Taux de prolactine (10 femmes)
Taux de prolactine (9 femmes)

Principe

Les tests d'hypothèses permettent de comparer des populations entre elles au moyen d'échantillons ou encore de comparer un échantillon avec une population de référence...

Types de tests d'hypothèses

Les tests d'hypothèses permettent de comparer des populations entre elles au moyen d'échantillons ou encore de comparer un échantillon avec une population de référence...

Dans le cadre de ces travaux pratiques, nous envisagerons trois types de tests d'hypothèses :

  1. test de comparaison d'une moyenne à un standard (1 échantillon)
  2. test de comparaison de 2 moyennes : 2 échantillons indépendants
  3. test de comparaison de 2 moyennes : 2 échantillons non indépendants ou observations pairées

Les tests 2 et 3 peuvent être également traités par l'ANOVA.

Les hypothèses

Quel que soit le type de tests (voir ci-dessus), on formule l'hypothèse de référence que les moyennes comparées proviennent d'une seule population de moyenne µ. Il s'agit de l'hypothèse de départ appelée "hypothèse nulle" (H0) qui pourra s'écrire comme suit dans le cas d'une comparaison de deux moyennes:

TeX Embedding failed!


Le contraire de l'hypothèse nulle est qu'une des populations possède une moyenne plus grande, plus petite ou tout simplement différente par rapport à l'autre population. Il s'agit de l'"hypothèse alternative" (H1) qui pourra s'écrire comme suit:

TeX Embedding failed!
ou TeX Embedding failed!
ou encore TeX Embedding failed!

 Les statistiques aident l'expérimentateur à choisir entre l'hypothèse nulle et l'hypothèse alternative

 

Réalisation du test

Réduction des moyennes observées:
En considérant l'hyptohèse nulle vraie, la (les) moyenne(s) mx obtenue(s) pour (les) l'échantillon(s) peu(ven)t être réduite(s) en une valeur observée (z observée ou t observée). Celle-ci peut ensuite être comparée à une valeur seuil (z table ou t table).

Recherche d'une limite arbitraire, une valeur seuil:

La valeur seuil va déterminer sous la courbe de Gauss réduite des zones distinctes: une zone probable suivant H0 et une zone peu probable suivant H0. Cette valeur seuil est déterminée par la valeur de alpha, choisie arbitrairement à 5%, 1% ou 0,1%. Le alpha choisi détermine donc une zone de valeurs de z ou de t peu probables sous H0.

Comparer la valeur réduite observée à la valeur seuil trouvée dans les tables:

Si l'hypothèse alternative H1 est " µ2 plus grand que  µ1"

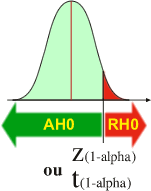
Lorsque la valeur observée (Z observée ou t observée) est plus grande que la valeur seuil (Z(1-alpha) ou t(1-alpha)), l'H0 est rejetée. La valeur observée est trop différente de la valeur attendue sous H0 pour considérer qu'elle est due au hasard de l'échantillonnage.

Dans le cas d'un rejet de H0 (RH0), l'expérimentateur aura réussi à démontrer que les moyennes observées sont telles que µ2 est vraisemblablement plus grande que  µ1. Comme la valeur de alpha choisie par l'expérimentateur est faible (maximum 5%), un RH0 signifie que la distance qui sépare les moyennes comparées est trop grande pour être simplement due au hasard. Le risque de se tromper lorsqu'on rejette RH0 est au maximum égal à alpha et si la valeur de z ou de t est très éloignée de la valeur seuil , la probabilité de se tromper est de loin inférieure à alpha. Dans ce cas, l'expérimentateur est quasiment "certain" que µ2 est bien plus grand que µ1.

Dans le cas d'une acceptation de H0 (AH0), rien ne permet à l'expérimentateur de dire que les moyennes sont différentes. Cette AH0 doit être considérée par l'expérimentateur comme une expérience non interprétable ou "non significative". A la différence de la "quasi certitude" au sujet de la conclusion tirée quand RH0, dans le cas d'une AH0, rien ne permet à l'expérimentateur d'être certain que les moyennes comparées sont effectivement identiques.

 

Si l'hypothèse alternative H1 est " µ2 plus petit que  µ1"

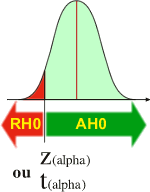
Lorsque la valeur observée (Z observée ou t observée) est plus petite que la valeur théorique (Z(alpha) ou t(alpha)), alors H0 est rejetée (RH0).

Dans le cas d'un rejet de H0 (RH0), l'expérimentateur peut affirmer que  µ2 est plus petit que  µ1 avec une probabilité de se tromper de alpha (maximum 5%).

Dans le cas d'une acceptation de H0 (AH0), l'expérimentateur n'a pas réussi à démontrer que  µ2 est plus petite que  µ1. La différence observée entre les moyennes d'échantillon pourrait s'expliquer par le jeu aléatoire de l'échantillonnage.

Si l'hypothèse alternative H1 est " µ2 différent de  µ1"

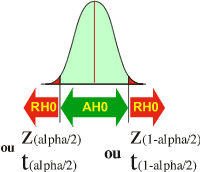
Lorsque la valeur observée (Z observée ou t observée) est SOIT plus petite que la valeur théorique (Z(alpha/2) ou t(alpha/2)), SOIT plus grande que la valeur théorique (Z(1-alpha/2) ou t(1-alpha/2)), alors H0 est rejetée (RH0).

Dans le cas d'un rejet de H0 (RH0), l'expérimentateur peut affirmer que µ2 est différent de µ1 avec une probabilité de se tromper de alpha (maximum 5%).

Dans le cas d'une acceptation de H0 (AH0), l'expérimentateur n'a pas réussi à démontrer que  µ2 est différent de µ1. La différence observée entre les moyennes d'échantillon pourrait s'expliquer par le jeu aléatoire de l'échantillonnage.

Test de comparaison d'une moyenne d'un échantillon par rapport à une population standard

Principe:

Un échantillon est prélevé et sa moyenne est calculée (mx). Cet échantillon provient-il d'une population 1 déterminée de moyenne µ1 ou bien appartient-il à une seconde population appelée population 2 de moyenne µ2? Autrement dit, cet échantillon est-il conforme à la population d'origine?

Retour

Les hypothèses:

Retour

Hypothèse nulle H0:

La moyenne de l'échantillon appartient à la population de référence de moyenne µ1.

TeX Embedding failed!

Retour

Hypothèse alternative H1:

  • L'échantillon appartient à une population dont la moyenne µ2 est supérieure à la moyenne µ1 de la population de référence.
    TeX Embedding failed!
  • ou encore: L'échantillon appartient à une population dont la moyenne µ2 est inférieure à la moyenne µ1 de la population de référence.
    TeX Embedding failed!
  • ou encore: L'échantillon appartient à une population dont la moyenne µ2 est différente de la moyenne µ1 de la population de référence.
    TeX Embedding failed!
Retour

Calculer la valeur observée:

Retour

Cas 1: la variance de la population de référence est connue:

La réduction de la moyenne de l'échantillon peut se faire par le calcul d'une valeur de Z observée dont la formule est la suivante:

TeX Embedding failed!

Où mx est la moyenne de l'échantillon; µ1 est la moyenne de la population de référence; TeX Embedding failed!  est la variance de la population de référence; n est la taille de l'échantillon.

Dans la table de Z, on trouve la (les) valeur(s) seuil(s) en tenant compte de alpha et du sens de l'hypothèse alternative (test uni- ou bi-directionnel).

  • AH0 : L'échantillon de moyenne mx appartient à la population de référence dont la moyenne est µ1.
  • RH0 : L'échantillon de moyenne mx n'appartient pas à la population de référence dont la moyenne est µ1 mais à une population dont la moyenne µ2 est plus grande OU plus petite que celle de la population de référence de moyenne µ1.
Retour

Cas 2: la variance de la population de référence est inconnue:

Dans ce cas, il n'est plus possible de calculer directement une valeur de z observée car il nous manque la valeur de la variance de la population de référence TeX Embedding failed!.

Cependant, il est possible d'adapter cette formule en estimant TeX Embedding failed! par la variance TeX Embedding failed! de l'échantillon. La variable réduite ainsi obtenue n'est plus une variable z mais une variable t avec n-1 degrés de liberté .

TeX Embedding failed!

Où mx est la moyenne de l'échantillon; µ1 est la moyenne de la population de référence; TeX Embedding failed! est la variance de l'échantillon, estimateur de la variance de la population (autrement dit la TeX Embedding failed! ); n est la taille de l'échantillon.

Pour trouver la ou les valeurs seuil, il faut donc rechercher la valeur t dans les tables de t de Student (l'aspect de la courbe est aussi une courbe de Gauss) en tenant compte de alpha (ou 1-alpha) et du nombre de dégrés de liberté:

tseuil;(n-1) degrés de liberté

Où "seuil" dépend du alpha choisi et du sens de l'hypothèse alternative; n est la taille de l'échantillon.

  • AH0 : L'échantillon de moyenne mx appartiendrait à la population de référence dont la moyenne est µ1 jusqu'à preuve du contraire.
  • RH0 : L'échantillon de moyenne mx n'appartient pas à la population de référence dont la moyenne est µ1 mais à une population dont la moyenne µ2 est plus grande OU plus petite que celle de la population de référence, dont la moyenne est µ1. 
Retour

Test de comparaison de 2 moyennes : 2 échantillons indépendants

 

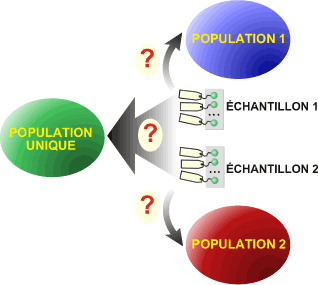
Principe:

Un expérimentateur désire comparer les moyennes (m1 et m2) de deux échantillons composés d'individus distincts: les individus de l'échantillon 1 ne sont pas les mêmes que ceux de l'échantillon 2! Les deux échantillons sont indépendants.

La question est: les deux échantillons proviennent-ils d'une seule population de moyenne µ ou proviennent-ils de deux populations distinctes de moyennes µ1 et µ2?

Cette analyse peut être réalisée par une ANOVA I à deux niveaux.

Retour

Les hypothèses

Retour

Hypothèse nulle H0

Les moyennes des échantillons appartiennent à une seule population de référence de moyenne Mx.

TeX Embedding failed!

Retour

Hypothèse alternative H1

  • Les moyennes des échantillons appartiennent à 2 populations distinctes. La population 1 a une moyenne µ1 supérieure à la moyenne µ2 de la population 2.
    TeX Embedding failed!
  • ou encore: Les moyennes des échantillons appartiennent à 2 populations distinctes. La population 1 a une moyenne µ1 inférieure à la moyenne µ2 de la population 2.
    TeX Embedding failed!
  • ou encore: Les moyennes des échantillons appartiennent à 2 populations distinctes. La population 1 a une moyenne µ1 différente de la moyenne µ2 de la population 2.
    TeX Embedding failed!
     
Retour

Calculer la valeur observée:

Retour

Cas 1: les variances des populations 1 et 2 sont connues:

La réduction de la différence des moyennes des échantillons peut se faire par le calcul d'une valeur de Z observé dont la formule est la suivante:

TeX Embedding failed!

Où m1 et m2 sont les moyennes des 2 échantillons; TeX Embedding failed! et TeX Embedding failed! sont les variances des 2 populations 1 et 2; n1 et n2 sont les tailles respectives des échantillons 1 et 2.

Trouvez dans les tables de Z, la ou les valeurs seuil en tenant compte de alpha et de H1.

  • AH0 : Les échantillons de moyenne m1 et m2 appartiennent à une seule population de référence dont la moyenne est µ.
  • RH0 : Les échantillons de moyenne m1 et m2 n'appartiennent pas à la même population de référence dont la moyenne est µ mais appartiennent à 2 populations distinctes dont les moyennes respectives µ1 et µ2 sont telles que µ1 est plus grande OU plus petite OU différente par rapport à µ2.
Retour

Cas 2: les variances des populations 1 et 2 sont inconnues:

Dans ce cas, il n'est plus possible de calculer directement une valeur de z observée les variances des populations de référence TeX Embedding failed! et TeX Embedding failed! sont inconnues. On peut néanmoins estimer ces dernières à partir des variances des échantillons, TeX Embedding failed! et TeX Embedding failed!.

Une question préalable doit être posée: La variabilité des 2 échantillons est-elle comparable, homogène? En d'autres termes, il faut vérifier l'égalité des variances des 2 populations étudiées, c'est-à-dire l'homoscédasticité. En effet si les variances sont hétérogènes, la différence de variances risque d'être confondue avec une différence de moyennes.

2.1: Test sur l'homogénéité des variances des échantillons comparés
  • Hypothèse nulle: Les variances des populations comparées sont homogènes.
    TeX Embedding failed!
  • Hypothèses alternatives pour 2 variances:
    • La variance 1 est plus grande que la variance 2.
      TeX Embedding failed!
    • La variance 2 est plus grande que la variance 1.
      TeX Embedding failed!
    • La variance 2 est différente la variance 1.
      TeX Embedding failed!

Pour réaliser ce test, l'expérimentateur établit le rapport entre la variance maximale et la variance minimale. Ce rapport est une valeur appelée F observé que l'on peut comparer avec une valeur F des tables de Fisher (voir Module 125 : page 3 : Test de Fisher).

TeX Embedding failed!
si TeX Embedding failed! est plus grande que TeX Embedding failed!.

L'expérimentateur va ensuite comparer cette valeur à une valeur théorique des tables de F de Fisher-Snedecor. En général, on utilise un test bidirectionnel avec une confiance de 95% (alpha=0,05). Le seuil est donc fixé à TeX Embedding failed!.

L'expérimentateur doit sélectionner la table où P(F < f) = 0,975.
Les degrés de liberté du numérateur (n1-1) dl correspondent à ceux de l'échantillon dont la variance est la plus grande. Ils permettent de rentrer en tête de colonne dans la table.
Les degrés de liberté du dénominateur (n2-1) dl correspondent à ceux de l'échantillon dont la variance est la plus petite. Ils permettent de rentrer en tête de ligne dans la table.

Fthéorique;(n1-1)dl;(n2-1)dl;0,975

  • AH0 si Fobservé est plus petit que Fthéorique: Les variances des populations d'où sont issues les échantillons sont considérées comme homogènes et l'expérimentateur peut alors envisager de comparer les moyennes des populations d'où sont issus les échantillons.
  • RH0 si Fobservéest plus grand que Fthéorique : Les variances des populations d'où sont issues les échantillons sont considérées comme hétérogènes. Il est alors IMPOSSIBLE de comparer par la suite les moyennes pour des échantillons dont les variances ne sont pas homogènes. Dans de nombreux cas, une transformation X'=log(x) ou X'=racine(x) permet d'homogénéiser les variances.
2.2: Test de comparaison des moyennes des 2 populations d'où proviennent les 2 échantillons

CONDITION: Ce test d'hypothèses portant sur les moyennes n'est possible QUE SI l'homogénéité des variances des populations a été confirmée par le test détaillé au point précédent

Les hypothèses H0 et H1 sont celles décrites plus haut.

L'expérimentateur va ensuite calculer une valeur de t observé: Dans cette formule, par rapport à celle du Z observé détaillée ci dessus, on remplacera TeX Embedding failed! et TeX Embedding failed! par une seule variance appelée "variance résiduelle" Sr² obtenue à partir des variances des deux échantillons TeX Embedding failed! et TeX Embedding failed!.

TeX Embedding failed!
avec
TeX Embedding failed!

Où m1 et m2 sont les moyennes des 2 échantillons; S2r est la variance résiduelle ; n1 et n2 sont les tailles respectives des échantillons 1 et 2, TeX Embedding failed! et TeX Embedding failed! sont les variances respectives des deux échantillons 1 et 2.

Ensuite, il reste à trouver dans les tables de t de Student (l'aspect de la courbe est aussi une courbe de Gauss), la ou les valeurs seuil en tenant compte de alpha et de H1. La valeur de t de Student nécessite aussi la détermination d'un certain nombre de degrés de liberté. Pour trouver la ou les valeurs seuil, il faut donc rechercher:

tseuil;(n1+n2-2) degrés de liberté

Où "seuil" peut être (1-α) ou α ou (1-α/2) ou (α/2) en fonction de l'hypothèse alternative; n1 et n2 les tailles des 2 échantillons.

  • AH0 : Les échantillons 1 et 2 appartiendraient, jusqu'à preuve du contraire, à des populations dont les moyennes µ1 et µ2 seraient égales.
  • RH0 : Les échantillons 1 et 2 appartiennent à deux populations dont les moyennes µ1 et µ2 seraient différentes (OU µ1 plus petite OU plus grande que µ2). 
Retour

Test de comparaison de deux moyennes (observations pairées)

Principe:

Un expérimentateur dispose d'une série d'observations associées par paires ou par couples. Par exemple, une expérience a été menée sur des rats. Ils ont été pesés avant et après un traitement hautement énergétique. A chaque individu de l'expérience est associée une pesée avant et après le traitement. Les données "avant" et "après" ne sont pas indépendantes et ne constituent donc pas des échantillons indépendants.

Pour traiter ce genre de test, l'expérimentateur doit considérer la différence de chaque couple de données. Toutes ces différences forment un échantillon dont on peut calculer la moyenne mD et la variance TeX Embedding failed!.

A partir de ce moment, l'expérimentateur dispose d'une seule série de n observations, supposée par H0 prise dans une population de moyenne µD, de variance inconnue estimée par TeX Embedding failed!, et souhaite éprouver H1 (µD > 0) et/ou H1 (µD < 0).

Remarque: ce test peut aussi être réalisé par la technique de l'ANOVA II, avec un critère fixe à deux niveaux croisés et un critère aléatoire à n niveaux.

Les hypothèses

Hypothèse nulle (H0)

TeX Embedding failed!
La moyenne des différences est égale à TeX Embedding failed! ou est nulle.

NB: En général delta vaut 0; il est rare que l'on souhaite tester une différence particulière, non nulle, mais c'est néanmoins réalisable.

Hypothèse alternative H1:

  • TeX Embedding failed!
    La moyenne des différences de la population de référence est plus grande que 0.
  • TeX Embedding failed!
    La moyenne des différences de la population de référence est plus petite que 0.
  • TeX Embedding failed!
    La moyenne des différences de la population de référence est non nulle.

Calculer la valeur observée:

La réduction de la moyenne des différences peut se faire par le calcul d'une valeur de t observé dont la formule est la suivante:

TeX Embedding failed!

Où mD est la moyenne des différences des données pairées; TeX Embedding failed! est la variance des différences des données pairées; n est le nombre de couples de données.

Trouvez dans les tables de t, la ou les valeurs seuil(s), en tenant compte d'alpha pour un test unidirectionnel ou bidirectionnel. Le nombre de degrés de liberté à employer est (n-1) dl où n est le nombre de couples de données.

tseuil, (n-1) dl; (1-α/2)

  • AH0 : La moyenne des différences de la population de référence est nulle.
  • RH0 : La moyenne des différences de la population de référence est non nulle.

ANalysis Of VAriance (ANOVA)

La réalisation d'un test d'Analyse de la Variance est une matière complexe, qui fera l'objet de plusieurs autres modules indépendants.

Pour savoir si vous devez ou non les parcourir, veuillez vous référer au programme de votre section ou de votre finalité.

  1. L'ANOVA 1 (module 140): principe, conditions d'utilisation, mise en oeuvre, interprétation et comparaison préalable des variances
  2. Tests complémentaires:
    1. Contrastes de Scheffé (module 150)
    2. Contrastes orthogonaux (module 160)
  3. La régression dans l'ANOVA1 (module 170)
  4. L'ANOVA 1 aléatoire (module 180)
  5. L'ANOVA et les critères de classification (module 190)
  6. L'ANOVA2 croisée fixe (module200)
  7. L'ANOVA et les modèles (module 210)

Formulaire relatif aux tests d'hypothèses: les moyennes

Comparer une moyenne à un standard

  Si la variance de la population standard (VARx) est connue Si la variance de la population standard (VARx) est inconnue
  TeX Embedding failed! TeX Embedding failed!
  H0: M1 = M2 = Mx
H1: M1 plus grand que M2 Z tables; (1-alpha) t tables; (n-1) dl; (1-alpha)
H1: M1 plus petit que M2 Z tables; (alpha) t tables; (n-1) dl; (alpha)
H1: M1 différent de M2

Z tables; (alpha/2)

Z tables;(1-alpha/2)

t tables; (n-1) dl; (alpha/2)

t tables;(n-1) dl; (1-alpha/2)
Retour

Comparer 2 moyennes d'échantillons provenant de 2 populations indépendantes:

  Si les variances des populations (VAR1 et VAR2) sont connues Si les variances des populations (VAR1 et VAR2) sont inconnues
  TeX Embedding failed!

TeX Embedding failed!
avec
TeX Embedding failed!
  H0: M1 = M2 = Mx
H1: M1 plus grand que M2 Z tables; (1-alpha) t tables; (n1+n2-2) dl; (1-alpha)
H1: M1 plus petit que M2 Z tables; (alpha) t tables; (n1+n2-2) dl; (alpha)
H1: M1 différent de M2

Z tables; (alpha/2)

Z tables;(1-alpha/2)

t tables; (n1+n2-2) dl; (alpha/2)

t tables;(n1+n2-2) dl; (1-alpha/2)
Retour

Comparer deux moyennes (observations pairées)

La variance de la population (VARD) est toujours inconnue
TeX Embedding failed!
H0: MD = delta
La moyenne des différences de la population de référence est nulle.

H1: MD est différente de delta
La moyenne des différences de la population de référence est non nulle.

t tables, (n-1) dl; (1-alpha/2) avec n nombre de couples

 

Retour

Hypothèses et prise de décision

Hypothèse nulle

H0: M1 = M2 = Mx

Hypothèses alternatives

H1: M1 plus grand que M2

AH0 si

  • Z observé plus petit que Z (1-alpha)
  • t observé plus petit que t (1-alpha)

RH0 si

  • Z observé plus grand que Z (1-alpha)
  • t observé plus grand que t (1-alpha)

H1: M1 plus petit que M2

AH0 si

  • Z observé plus grand que Z (alpha)
  • t observé plus grand que t (alpha)

RH0 si

  • Z observé plus petit que Z (alpha)
  • t observé plus petit que t (alpha)

H1: M1 différent de M2


AH0 si

  • Z observé compris entre Z (alpha/2) et Z (1-alpha/2)
  • t observé compris entre t (alpha/2) et t (1-alpha/2)

RH0 si

  • Z observé plus grand que Z (1-alpha/2)
  • t observé plus grand que t (1-alpha/2)

ou

  • Z observé plus petit que Z (alpha/2)
  • t observé plus petit que t (alpha/2)

Exercices

1. Un laboratoire étudie l'influence d'un contraceptif X sur un groupe de 18 femmes de 25 ans. Chez la femme, au "jour 14 " du cycle menstruel, une augmentation de la concentration en LH (Luteinizing Hormone) induit l'ovulation. A ce stade précis, la concentration en LH est une v.a.N(14,5; 5,0625). Pour l'échantillon de 18 femmes, on obtient une moyenne de 13,03 mIU/ml et une variance de 6,32 (mIU/ml)². La prise du contraceptif X a-t-elle une influence (significative (alpha =5%) ou hautement significative (alpha =1%)) sur la concentration en LH et sur l'ovulation ?

2. Des études comparatives sur la fécondité des femmes au sein de la communauté européenne ont été menées sur des femmes de 40 ans. Pour cela, un statisticien a réalisé deux échantillons: l'un (de 100 femmes) en France, l'autre (de 80 femmes), en Belgique. Il a obtenu une moyenne de 1,78 enfants / femme et une somme de carrés d'écarts (SCE) de 427,68 (enfants / femme)² pour l'échantillon français et une moyenne de 2,12 enfants / femme et une SCE de 281,24 (enfants / femme)² pour l'échantillon belge. Les femmes françaises sont-elles moins fécondes que leurs homologues belges?

3. Dans une fabrication de boulons pour machines, l'ingénieur du contrôle-qualité trouve qu'un échantillon de taille n = 100 est nécessaire pour détecter des changements fortuits de 0,5mm dans la longueur moyenne du boulon fabriqué. Supposons qu'il souhaite une précision plus grande pour détecter un changement de 0,1mm seulement, avec les mêmes erreurs de type I et II. De combien doit-il augmenter la taille de son échantillon ? (c'est facile si on reformule le problème en terme d'intervalles de confiance. Pour construire un intervalle de confiance 5 fois plus précis, de combien doit-on augmenter la taille de l'échantillon ?)

4. Des études de consommation ont été réalisées en Irlande et en Angleterre. Les dépenses en services médicaux et dépenses de santé représentaient, en 1985, respectivement 1,5% et 1% de la consommation totale des ménages. Sachant qu'en Europe, la variation des dépenses en services médicaux et dépenses de santé est de 1,9 (%²), combien de ménages doit-on étudier (alpha = 5%) dans ces deux pays pour montrer, dans 99% des cas, que la consommation totale en Irlande est supérieure à celle obtenue en Angleterre ?

5. Pour deux catégories différentes de raisins (catégorie 1 et catégorie 2), on a observé l’acidité (pH) de 7 et de 11 grappes respectivement. On remarque que l’échantillon de la catégorie 1 a une acidité moyenne de 3.556 (variance 0.011) et celle de l’échantillon de la catégorie 2 est de 3.477 (variance 0.007). Testez si la différence est significative.

6. Un procédé de fabrication courant a produit des millions de tubes T.V., dont la durée de vie moyenne est µ=1200 heures et l’écart-type σ = 300 heures. Un nouveau procédé, estimé meilleur par le bureau d’études, fournit un échantillon de 100 tubes avec une moyenne de 1265. Bien que cet échantillon fasse apparaître le nouveau procédé comme meilleur, s’agit-il d’un coup de chance de l’échantillonnage?

7. Un enseignant réalise la même interrogation dans deux groupes de 17 étudiants d’une même section. Le groupe A obtient une moyenne sur 20 de 13,1 ± 4,16 et le groupe B obtient une moyenne de 10.8 ± 1,92. Les deux groupes sont-ils de force équivalente (avec un alpha de 5%)? Un troisième groupe (groupe C) de cette section de 17 individus est également testé et la moyenne obtenue vaut 9.8 ± 3.86. Le groupe C est-il moins fort que le groupe A (avec un alpha de 5% et de 1%)? En est-il de même par rapport au groupe B (avec un alpha de 5% et de 1%)?

8. Un étudiant en biologie clinique désire comparer deux méthodes d'analyse des triglycérides sur 10 patients. Une moitié de chaque prélèvement est testée par la méthode A et il note une concentration moyenne de triglycérides de 102.3 mg/dl pour une variance de 7.68 (mg/dl)². L'autre moitié est testée par la méthode B et il observe une concentration moyenne de 107.5 mg/dl pour une variance de 6.23 (mg/dl)². En moyenne la différence enregistrée dans l'échantillon de 10 patients est de 3.75 mg/dl pour une variance de 13.2 (mg/dl)². Ces deux méthodes donnent-elles des résultats comparables avec un seuil de signification de 5%? Sinon, qu'en est-il à 1%?

9. Un biologiste teste 2 techniques de mesure de température sur un troupeau de 30 vaches. La première technique utilise un thermomètre conventionnel au mercure et la seconde utilise un appareil à détection infrarouge à distance. Les 2 techniques donnent respectivement 38.7 ± 0.54 °C et 38.9 ± 0.64°C. La différence moyenne entre les deux techniques est de 0.16 ± 0.44°C. Quelles conclusions pouvez-vous tirer?

10. Un physiologiste étudie l'influence du cadmium sur le taux de glucose dans le sang. Il remplit 2 bassins avec d'une part de l'eau de distribution et d'autre part de l'eau de distribution à laquelle on a ajouté une dose de 0.01mg de Cd par litre. 18 truites sont disposées dans ces 2 bassins et le taux de glucose dans le sang est mesuré après 2 heures d'incubation. Les résultats sont représentés dans le tableau ci-dessous:

 

bassin sans Cd ajouté

bassin avec 0.01mg Cd/l

différence avec/sans Cd

moyenne

86.6

91.2

4.6

variance

5.1

8.3

3.2

Les variances attendues dans le bassin sans Cd étant de 5 et de 10 dans le bassin traité, le cadmium augmente-t-il la glycémie chez les truites (faire le test avec un seuil de signification de 5% et de 1%)?

11. Apparentée aux races anglaises KERRY, DEVON, JERSEY, GUERNESEY, la race BRETONNE PIE NOIRE a été façonnée par le climat et le sol bretons. Cette race est exploitée en Bretagne et dans les départements limitrophes. Elle reste, parmi les races françaises, une de celles ayant le mieux conservé ses caractères originels, l’impact des croisements ayant été faible au siècle dernier. 

De récents croisements ont été réalisés afin d'accroître ses performances au niveau de leur production de viande. Ci-dessous, voici les résultats des tests effectués sur des individus provenant du croisement de cette race avec une race déterminée.

  échantillon Pie-Noire échantillon croisé SCE
pie noire vs croisement 1

moyenne = 601,66
variance = 181,53
nb individus = 18

moyenne = 611,57
variance = 258,54
nb individus = 18

 SCEF = 884,08
SCER = 7481,18
pie noire vs croisement 2

moyenne = 598,13
variance = 192,55
nb individus = 18

moyenne = 609,19
variance = 294,43
nb individus = 18

 SCEF = 1101,68
pie noire vs croisement 3

moyenne =595,85
variance = 142,48
nb individus = 18

moyenne = 622,24
variance = 514,10
nb individus = 18

 SCEF = 6263,96
SCER = 11161,87

Les différents croisements donnent-ils des résultats plus performants que la race pure (alpha de 5% et 1%)? [Note: considérer chaque ligne du tableau comme une nouvelle expérience]

12. Une industrie pharmaceutique désire tester trois stimulants de l'appétit (S1, S2, S3) en mesurant la capacité d'absorption de nourriture chez le rat. Quatre groupes de 12 rats sont constitués: le premier servant de témoin, les trois autres recevant respectivement les stimulants S1, S2 et S3. On mesure la quantité de nourriture (en kg) ingérée sur un mois. Que peut-on conclure?

 
Témoin
S1
S2
S3
Moyennes
2,90
4,11
5,14
5,56
Variances
2,11
0,99
0,35
1,05

On sait aussi que la variance factorielle est de 16,90 et la variance résiduelle est de 1,13.

13. Un ornithologue s'intéresse à l'évolution d'une espèce d'oiseaux répartie dans trois sites géographiquement distincts A, B et C, et plus particulièrement aux différences morphologiques engendrées par les mécanismes d'isolement. A cet effet, il a mesuré la longueur des ailes (en mm) de 10 oiseaux capturés sur chaque site. Les barrières géographiques ont-elles engendré des différences morphologiques sur cette espèce?

 
A
B
C
Moyennes
71,2
74,4
72,6


On sait que la variance résiduelle: 4,31. [On considère que les échantillons sont comparables au niveau de la variabilité entre échantillons]

14. Douze parcelles de terrain sont divisées aléatoirement en 3 groupes. Le premier sert de témoin, les deux autres sont fertilisés respectivement avec les engrais A et B. Les rendements observés sont les suivants. Les engrais affectent-ils la production?

  Témoin A B
Moyennes 61 70 73
Variances 20,6 14 17,3

On sait que la variance expliquée est de 156 et que la variance non expliquée est de 17,3.

15. Pour définir l'impact de la nature du sol sur la croissance d'une plante X, un botaniste a mesuré la hauteur des plantes pour 4 types de sol. Pour chaque type de sol, il disposait de 3 réplicats.

 

Type de sol
  I II III IV
  15 25 17 10
  9 21 23 13
  4 19 20 19
Moyennes 9,33 21,67 20,00 14,00
variances 30,33 9,33 9,00 21,00

Sachant que la variance expliquée par la nature du sol est de 96,31 et que la variance résiduelle est de 17,42, que peut-on conclure sur cette expérience?

16. Dans le cadre d'une étude écotoxicologique, la concentration en DDT et en ses dérivés a été mesurée chez des brochets de différents âges. Les résultats obtenus sont donnés, dans le tableau ci-dessous pour des échantillons de 11 individus chacun.

  2 ans 3 ans 4 ans 5 ans 6 ans
moyennes 0,18300 0,33763 0,45113 0,70738 1,19750
variances 0,00035 0,00106 0,00024 0,00045 0,00125

Sachant que la variance expliquée par l'âge des brochets est de 1,260770 et que la variance résiduelle est de 0,000672, que peut-on conclure sur cette étude?