Optimisation d'une expérience: augmenter alpha

Comment optimiser une expérience pour voir un effet le plus souvent possible?

4. Augmenter alpha

Pour diminuer le recouvrement entre les distributions H0 et H1, l'expérimentateur pourrait être tenté d'augmenter la surface alpha afin d'accroître la puissance (1-β). Cette pratique n'est cependant pas recommandée. En effet, l'expérimentateur se doit de diminuer parallèlement les 2 types d'erreur, alpha et beta car il ne sait jamais au préalable quelle est la décision correcte (AH0 ou RH0).

L'expérimentateur délimite arbitrairement un intervalle de confiance (1-α) et une erreur de type I (α) mais par définition alpha doit être petit.

Soit il n'y a pas d'effet :

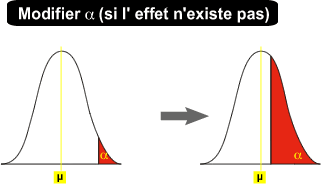
En augmentant alpha, l'expérimentateur rejettera plus souvent l'hypothèse nulle à tort.

Soit il y a un effet :

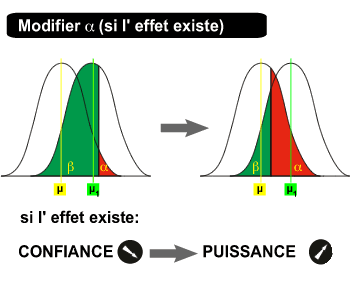
Si on réalise un test avec un grand alpha :

• En cas de RH0, la confiance est faible, le risque d'erreur de type I est grand (= alpha).
• En cas d'AH0, le risque d'erreur II est toujours inconnu.

 

En conclusion:

Si la valeur observée se retrouve dans la zone de rejet de l'hypothèse nulle, cela veut dire que:

1. l'expérimentateur a obtenu une valeur observée qui est très éloignée de la moyenne de la population de référence. La probabilité de l'obtenir par hasard dans cette population de référence est très faible mais pas impossible (probabilité < alpha)
2. La valeur observée est trop éloignée de la moyenne de la population de référence et l'expérimentateur en déduit qu'elle n'a pas été obtenue par hasard et, que par conséquent, le modèle H1 est très vraisemblable.

Remarques:

1. Si un expérimentateur réduit la surface alpha pour diminuer la probabilité d'erreur de type I, cela entraîne une diminution de la puissance.

2. Si un expérimentateur fixe un alpha nul, il considérera toujours une valeur observée même anormale comme conforme.

   Par exemple, si le alpha est très petit, le seuil de signification à atteindre pour considérer le poids d'un individu comme trop élevé est pratiquement impossible à atteindre. Le poids d'un sumo risque d'être assimilé à un poids tout à fait habituel chez un homme adulte alors qu'il devrait être considéré comme un obèse.

   

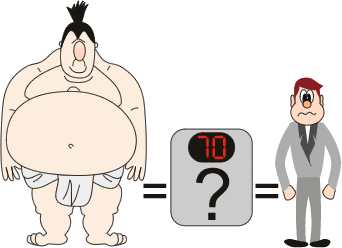
3.  L'erreur de type I (alpha) résulte donc d'un compromis

   •   alpha ne doit pas être trop grand. Si on rejette H0, il faut avoir une grande confiance en sa décision ou une probabilité d'erreur de type I faible (= alpha).

   • alpha ne doit pas être trop petit car s'il y a un effet à voir, le seuil de signification risque d'être impossible à atteindre vu son éloignement par rapport à la moyenne de la population de référence.