Tables de Chi-carré
La distribution de Χ2 est utilisée pour tester des statistiques basées sur le calcul de la somme des carrés des écarts
Les degrés de liberté déterminent la forme de la courbe et dépendent du nombre de catégories dans lesquelles les fréquences sont dénombrées.
Plus le nombre de degrés de liberté augmente, plus Χ2 tend vers une v.a. Normale.
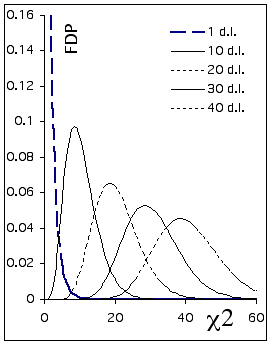
Figure - Comparaison de fonctions Χ2 avec différents nombres de degrés de liberté. La distribution de Χ2 avec un petit nombre de degrés de liberté est fortement asymétrique.
La table de Χ2 est généralement présentée de la façon suivante :
|
0.9 |
0.95 |
0.975 |
0.99 |
|
|
1 |
2.71 |
3.84 |
5.02 |
6.63 |
|
2 |
4.61 |
5.99 |
7.38 |
9.21 |
|
3 |
6.25 |
7.81 |
9.35 |
11.34 |
|
4 |
7.78 |
9.50 |
11.14 |
13.28 |
La première ligne énumère des probabilités, la première colonne, le nombre de degrés de liberté. Chaque cellule comprend la valeur de Χ2 telle que P[Χ2 < Χ2dl]=p , p étant la probabilité reprise en tête de colonne et dl le nombre de degrés de liberté repris en tête de ligne.
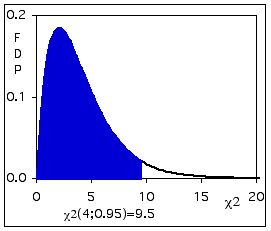
Figure - Illustration de la probabilité reprise dans la table, 4 d.l. p= 0.95.