Exemple
Imaginons un modèle qui répartisse les observations en trois catégories, par exemple les produits AA, Aa et aa de plusieurs croisements hétérozygotes, de probabilité 25%, 50% et 25% respectivement. Effectuons 5 fois l’expérience qui consiste à relever la fréquence de chaque phénotype :
|
N° |
AA |
Aa |
aa |
Χ2obs |
|
1 |
27 |
49 |
20 |
|
|
2 |
17 |
53 |
31 |
4.13 |
|
3 |
27 |
46 |
22 |
0.62 |
|
4 |
22 |
46 |
27 |
0.62 |
|
5 |
28 |
53 |
17 |
3.12 |
Comment sont calculées ces valeurs ?
Ligne 1: 27+49+20=96 données, ce qui donne des fréquences théoriques de 24, 48, et 24 (25%, 50%, 25% de 96).
Le Chi²observé est donc TeX Embedding failed!, c'est à dire 1.06 si on arrondit à deux chiffres significatifs.
Répétition de l’expérience, fréquences observées et valeurs de Chi²observé
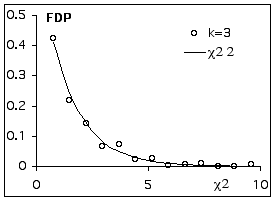
Comparaison des écarts quadratiques standardisés à la distribution théorique de Chi² avec deux degrés de liberté.
Considérons la probabilité a priori de 10 acides aminés de se trouver dans une hélice alpha et dénombrons leur fréquence dans 4 protéines.
|
Acide aminé |
Probabilité |
Protéines |
|||
|
1 |
2 |
3 |
4 |
||
|
Ile |
0.03 |
4 |
3 |
3 |
3 |
|
Asn |
0.05 |
8 |
5 |
8 |
4 |
|
Val |
0.07 |
12 |
7 |
8 |
4 |
|
Thr |
0.07 |
5 |
8 |
7 |
9 |
|
Tyr |
0.07 |
9 |
7 |
10 |
5 |
|
Leu |
0.13 |
8 |
15 |
15 |
12 |
|
Pro |
0.13 |
14 |
13 |
12 |
13 |
|
Glu |
0.15 |
9 |
18 |
16 |
17 |
|
Gly |
0.15 |
17 |
12 |
16 |
10 |
|
Met |
0.15 |
12 |
16 |
18 |
20 |
|
total |
1 |
98 |
104 |
113 |
97 |
|
Χ2obs |
12.32 |
1.49 |
2.35 |
6.40 |
|
Probabilités, fréquences observées et Chi² observé pour 10 acides aminés répertoriés dans les hélices alpha de 4 protéines.
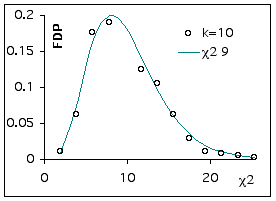
Si l’on répète l’expérience sur un plus grand nombre de protéines, on observe une distribution de Chi²observé qui peut se comparer à une distribution théorique de Chi² avec 9 degrés de liberté.