Principe
Imaginons un modèle qui répartisse les observations en deux catégories, par exemple mâles et femelles, dans une population de sex-ratio 0,5.
| TeX Embedding failed! |
Calculons un écart quadratique entre les fréquences observées et théoriques, standardisé par la fréquence théorique : TeX Embedding failed! et rassemblons les valeurs dans un tableau :
|
mâles |
femelles |
total |
|
|
fi observée |
23 |
64 |
87 |
|
fi théorique |
29 |
58 |
87 |
|
écart quadratique standardisé |
1.24 |
0.62 |
1.86 |
Les fréquences observées fobsi correspondent approximativement à des variables aléatoires de Poisson X=Po(m), où la moyenne m est égale à n.π (π = la probabilité d’appartenir à la catégorie i) ou encore égale à la fréquence théorique fthi .
La variance attendue de cette fréquence observée est donc Var(X)= m = n.π = fthi
La quantité TeX Embedding failed! est donc approximativement une variable Z(0 ;1).
L’écart global entre les observations et le modèle est calculé par la statistique
| TeX Embedding failed! |
| TeX Embedding failed! |
Si l’on répète l’expérience un grand nombre de fois, on obtiendra différentes fréquences, et différentes valeurs de Χ2obs.
|
Echantillon N° |
mâles |
femelles |
Χ2 obs |
|
2 |
29 |
62 |
0.0879 |
|
3 |
25 |
60 |
0.5882 |
|
4 |
25 |
73 |
2.6990 |
|
5 |
32 |
63 |
0.0053 |
|
6 |
37 |
66 |
0.3107 |
|
7 |
32 |
74 |
0.4717 |
Comparons les valeurs obtenues pour Χ2 obs avec k=2 (nombre de degrés de liberté=1) :
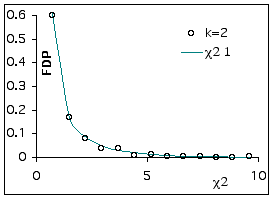
Comparaison des écarts quadratiques standardisés à la distribution théorique de khi-carré avec un degré de liberté.