Définition
La variable chi carré (Χ2) est une somme de variables aléatoires normales réduites au carré (une somme de z2). Sa distribution est asymétrique et dépend d'un seul paramètre k ou nombre de degrés de liberté. Ce nombre de degrés de liberté dépend du nombre de variables aléatoires normales indépendantes intervenant dans la somme.
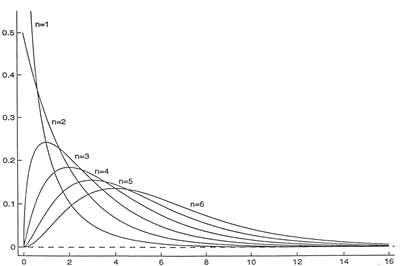
A partir de 3 degrés de liberté, les distributions Χ2 suivent une distribution en cloche caractérisée par une dissymétrie à gauche. La forme de la courbe est déterminée par le nombre de degrés de liberté. En effet, plus le nombre de degrés de liberté augmente, plus Χ2 tend vers une v.a. Normale et donc adopte une courbe en cloche.
La variable Χ2 est souvent utilisée dans les tests statistiques basés sur la somme des carrés des écarts (par exemple, somme de carrés d'écarts entre fréquences observées et fréquences théoriques).
Types de tests
Dans le cadre de ce cours de statistiques élémentaires, nous ne nous préoccuperons que de deux types de tests différents: