Réduction de variable

Chaque v.a. normale possède sa propre moyenne (µ) et variance (σ²). Déterminer des probabilités sous ce type de courbe de Gauss (à chaque cas particulier est associée une courbe de moyenne et de variance particulière) requiert un algorithme d'intégration numérique.

Heureusement, toutes les v.a. Normales peuvent se réduire à une seule et même distribution normale réduite Z. La distribution réduite de Z est centrée sur une moyenne 0 et possède une variance 1. La table de probabilité de Z a été calculée une fois pour toutes et dispense des probabilités du type:

P(Z ≤zi)

Comment réduire?

Toute v.a. normale peut être ramenée à une variable normale réduite Z v.a. N (0;1) par simple transformation algébrique (soustraction de la moyenne et division par l'écart-type). Cette opération est appelée réduction de la variable étudiée X en la variable réduite Z.

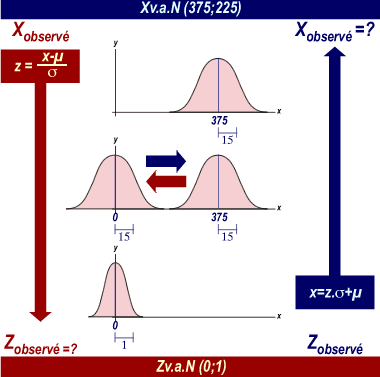
Convertir une valeur expérimentale (Xobservé) en une valeur réduite (Zobservé)

Xobservé = 390 et X v.a.N (375;225), alors TeX Embedding failed!

Convertir une valeur réduite (Zobservé) en une valeur expérimentale (Xobservé)

Zobservé = 2,5 et X v.a.N (375;225), alors TeX Embedding failed!