Propriétés

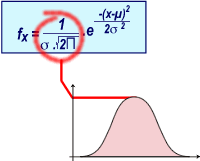
Equation et symbolique

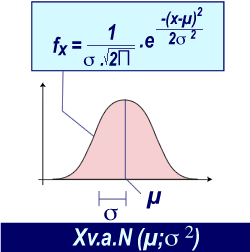
La fonction de densité de probabilités (fx) se caractérise par une équation faisant intervenir la moyenne µ et la variance σ². Par convention, nous adopterons la convention d'écriture: X v.a.N(µ;σ²) . Dans la littérature, on peut aussi trouver: µ±σ (moyenne ± écart-type).

Symétrie autour de la moyenne

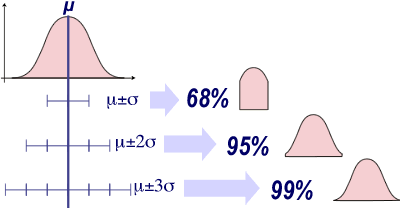
La courbe de Gauss-Laplace est symétrique:

1. Lorsqu'on sélectionne l'intervalle compris entre +1 et -1 écart-type autour de la moyenne µ (de μ-σ jusque μ+σ), on isole 68% des individus d'une population normale.
2. Lorsqu'on sélectionne l'intervalle compris entre +2 et -2 écarts-types autour de la moyenne µ (de μ-2σ jusque μ+2σ), on isole 95% des individus d'une population normale.
3. Lorsqu'on sélectionne l'intervalle compris entre +3 et -3 écarts-types autour de la moyenne µ (de μ-3σ jusque μ+3σ), on isole 99% des individus d'une population normale.

Modification de la variance

Lorsque la variance d'une population diminue, cela se traduit par une dispersion moins importante de la courbe autour de la moyenne. Parallèlement, le sommet de la courbe tend à s'élever afin de préserver une surface totale sous la courbe égale à 1 (ou 100%).

Exemple:

Dans une population de chauves-souris de l'espèce A, l'envergure X est une v.a. N(375; 225)
Dans une population de chauves-souris de l'espèce A femelles, l'envergure X est une v.a. N(375; 121)
Dans une population de chauves-souris de l'espèce A femelles de 3 mois, l'envergure X est une v.a. N(375; 49)
etc.

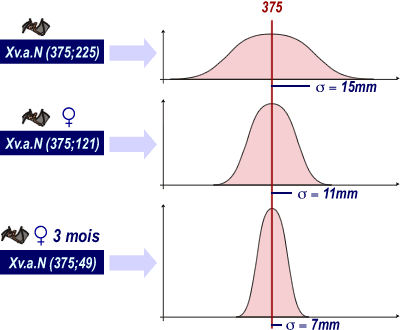
Influence de la variance sur le sommet de la courbe de Gauss: 

Si la variance diminue, le sommet de la courbe tend à augmenter. 

En effet, dans l'équation de la courbe, l'écart-type se trouve au dénominateur (voir terme entouré en rouge). Plus l'écart-type est petit, plus ce terme tend à devenir grand.