Principes du test d'hypothèses
Concept du test d'hypothèses
Tout expérimentateur est amené à se poser la question suivante:
La valeur obtenue dans un échantillon est-elle conforme à un modèle établi? Ou encore, cette valeur est-elle probable, étant donné un modèle supposé.
Par exemple, si la moyenne réelle de la pression sanguine de la population était de 120 mm Hg, est-il normal (probable) d'obtenir une moyenne d'échantillon de 140 mm Hg?
En disant cela on introduit la notion de test d'hypothèses.
Seuil de signification:
L'expérimentateur est amené à établir, suivant un seuil de confiance arbitraire, une limite (ou 2 limites) afin de séparer ce qu'il considère comme des valeurs conformes "probables" (la zone de confiance) et des valeurs non conformes "peu probables" (la zone d'erreur de type I). Cette limite s'appelle le seuil de signification. En termes de variable normale réduite et de test unidirectionnel, le seuil de signification a pour valeur, Z1-alpha, c'est-à-dire la valeur de la table de Z qui correspond à une probabilité de 1-alpha (test de conformité d'une moyenne à un standard avec variance connue).
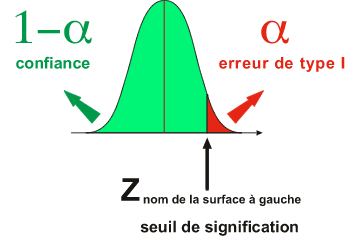
Seuil de signification
Pour répondre à cette question, l'expérimentateur va devoir définir arbitrairement une limite (une frontière) entre la conformité (en vert) ou événements probables et la non conformité à un modèle (en rouge) ou événements peu probables.
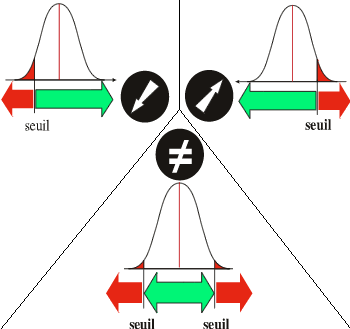
L'expérimentateur peut ainsi définir 3 types de limites selon l'hypothèse à tester:
 Test unidirectionnel à droite
Test unidirectionnel à droite
Seuil: Z1-α
Confiance: 1-α
L'expérimentateur désire tester si la statistique de l'échantillon est significativement supérieure à celle attendue : "L'individu mesuré ou la moyenne de l'échantillon sont-ils conformes (probables) ou significativement plus grands (peu probables) que prévus par le modèle?"
 Test unidirectionnel à gauche
Test unidirectionnel à gauche
Seuil: Zα
Confiance: 1-α
L'expérimentateur désire tester si la statistique de l'échantillon est significativement inférieure à celle attendue: "L'individu mesuré ou la moyenne de l'échantillon sont-ils conformes (probables) ou significativement plus petits (peu probables) que prévus par le modèle?"
 Test bidirectionnel
Test bidirectionnel
Seuils: TeX Embedding failed! et TeX Embedding failed!
Confiance: 1-α
L'expérimentateur désire tester si la statistique de l'échantillon est significativement différente de celle attendue, soit trop petite soit trop grande: "L'individu mesuré ou la moyenne de l'échantillon sont-ils conformes ou non (soit plus grands ou plus petits) au modèle?"
La zone correspondant à l'erreur de type I
En rouge :
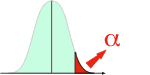
Elle constitue une zone de faible probabilité fixée par l'expérimentateur. En général, elle équivaut à 5%, 1% voire 0,1% de la surface totale sous la courbe de Gauss.
Pour qu'une mesure ou une moyenne se retrouve dans cette zone, il faut que sa valeur soit très éloignée du centre de la distribution µ (ou 0 si on travaille avec une variable normale réduite) au point de dépasser la valeur seuil xa.
Si tel est le cas, on suppose qu'il y a beaucoup de chances que cette mesure (ou cette moyenne) n'ait pas été obtenue par hasard (comme il y a moins de alpha chances d'obtenir une telle valeur). On en déduit que la mesure (ou la moyenne) provient d'une autre population (population 1) que celle prévue par le modèle H0, où la valeur observée est beaucoup plus probable. En décidant que le modèle H0 est invalide il y a cependant alpha % de chances de se tromper. Comme cet alpha est fixé par l'expérimenteur, le risque encouru ou erreur de type I est connu et peut être très petit.
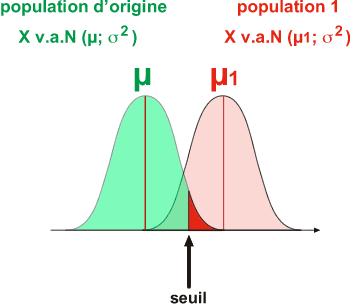
La zone de confiance
En vert :
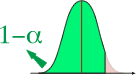
Une valeur comprise dans cette zone de confiance est considérée par l'expérimentateur comme une valeur tout à fait conforme au modèle H0 décrivant la population d'origine centrée sur la moyenne µ. La valeur est considérée comme probable et la différence observée par rapport à la moyenne µ du modèle H0 peut être atttribuée au hasard résultant de l'échantillonnage aléatoire.
Cette zone représente 95%, 99% voire 99,9% de la surface de la courbe de Gauss. La distance qui sépare la valeur observée de la moyenne µ du modèle H0 n'est pas suffisante pour être considérée comme non conforme ou "improbable" (car inférieure à la distance séparant µ du seuil de signification).
Dans cette zone, l'expérimentateur doit admettre que la valeur observée est conforme à la population centrée sur µ. Ce n'est pas pour autant que le modèle H0 est validé mais il n'a pas réussi à démontrer le contraire, c'est-à-dire que l'échantillon proviendrait d'une autre population centrée sur une autre moyenne.
La procédure à suivre dans un test d'hypothèses
1. Savoir d'où l'on part et ce qu'on souhaite démontrer
Un expérimentateur a mesuré un chevaine de 3 ans et veut le comparer à la population de chevaines de 3 ans centrée sur µ. Son point de départ est de dire que l'individu est conforme à cette population: c'est l'hypothèse nulle H0. Ce qu'il veut démontrer est SOIT:
- que le poisson mesuré est plus petit que prédit par la normale et appartient à une population centrée sur µ1 plus petite que µ (en vert)
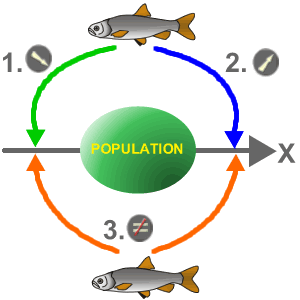
Dans ce cas, on peut poser les hypothèses suivantes: H0: µ = µ1 et H1: µ1 inférieure à µ. Il s'agira alors d'un test unidirectionnel à gauche. - que le poisson mesuré est plus grand que prédit par la normale et appartient à une population centrée sur µ1 plus grande que µ (en bleu)
Dans ce cas, on peut poser les hypothèses suivantes: H0: µ = µ1 et H1: µ1 supérieure à µ. Il s'agira alors d'un test unidirectionnel à droite. - que le poisson mesuré est ou plus grand ou plus petit (différent) que prédit par le modèle et appartient à une population centrée sur µ1 plus grande OU plus petite que µ (en orange)
Dans ce cas, on peut poser les hypothèses suivantes: H0: µ = µ1 et H1: µ1 différente de µ. Il s'agira alors d'un test bidirectionnel.
Le choix de l'hypothèse alternative H1 se fait en fonction des connaissances a-priori ou scientifiques de l'expérimentateur (par exemple, conditions d'élevage favorables ou défavorables) et NON en fonction de la valeur observée qui peut être inférieure ou supérieure à la valeur attendue simplement par le jeu de l'échantillonnage aléatoire.
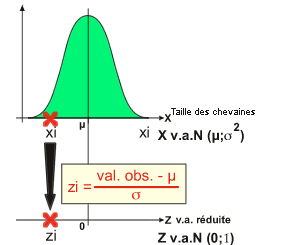
2. Convertir la valeur observée en une valeur réduite
L'expérimentateur a obtenu une taille pour le poisson capturé (ou une taille moyenne s'il en a capturé plusieurs). Pour faciliter sa prise de décision (Accepter le fait que ce poisson est normal [acceptation de H0 = AH0] ou non [rejet de H0 = RH0]), il va réduire la valeur observée en une valeur réduite (z réduit, t réduit, ...).
3. Rechercher dans les tables réduites correspondantes la ou les valeurs seuil:
En fonction du alpha déterminé par l'expérimentateur et de l'hypothèse H1 choisie, il va définir un seuil de signification particulier.
- Test unidirectionnel à gauche: Zα
- Test unidirectionnel à droite: Z1-α
- Test bidirectionnel: TeX Embedding failed! ou TeX Embedding failed!
Exemple
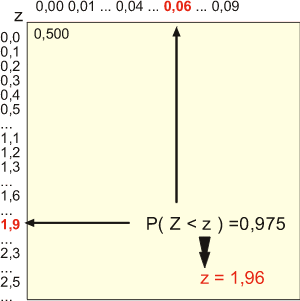
Soit une différence à mettre en évidence pour un alpha de 5% (test bidirectionnel: il y a donc 2 seuils à trouver Z0,025 et z0,975) .
Dans la table, on localise la valeur la plus proche de 0,975 afin de trouver z0,975. Le z trouvé dans les tables est de 1,96. Par symétrie, on peut déduire le z0,025: -1,96
Conclusion du test
En comparant la valeur réduite des observations (z observé) avec la valeur seuil trouvée dans les tables, l'expérimentateur peut tirer une conclusion à son test.
Exemple
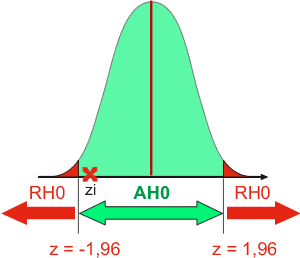
Soit une valeur de z observée de -1,84 pour un test bidirectionnel avec un alpha de 5%. Dans ce cas, -1,84 est compris entre -1,96 et 1,96. La valeur étant comprise entre les deux valeurs seuils, elle est considérée comme "normale". Cela revient à dire que la probabilité d'obtenir une valeur (1,84) aussi éloignée de 0 est plus grande que 5%. On considère donc que l'événement est probable sous H0 et que la valeur observée est due au hasard de l'échantillonnage.
La conclusion au test est la suivante: La différence entre la mesure observée et la valeur attendue peut être attribuée au hasard de l'échantillonnage. Par conséquent, on accepte l'hypothèse nulle (AH0).
Si la valeur observée n'était pas comprise entre -1,96 et 1,96, l'expérimentateur aurait pu conclure que la mesure observée était trop différente de la normale ou trop peu probable sous H0 (< 5%). Par conséquent, il aurait rejeté l'hypothèse nulle (RH0).
Remarque
Dans le cas d'un test bidirectionnel, RH0 signifie bien sûr la mise en évidence d'une différence de la valeur observée par rapport à la normale MAIS on peut aller plus loin. En effet, pour un même alpha MAIS pour un test unidirectionnel, on aura aussi un RH0. L'expérimentateur pourra donc dire qu'il y a une différence de la mesure mais aussi que celle-ci est plus grande ou plus petite que la normale.
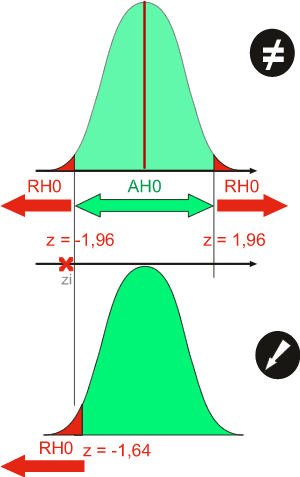
Attention: La conclusion inverse n'est pas vraie. Ce n'est pas parce qu'on rejette l'hypothèse nulle (RH0) dans un test unidirectionnel avec un alpha déterminé qu'il y a rejet de l'hypothèse nulle (RH0) pour un test bidirectionnel avec le même alpha.
Exercices
1. Un écologiste étudie une population de chauves-souris de l'espèce Grand Rhinolophe. D'après la littérature, il sait que l'envergure de ces chiroptères obéit à une distribution normale dont la moyenne est de 375 mm pour une variance de 225 mm2.
Cet écologiste capture un individu dont la taille est de 350 mm. Cet individu est-il considéré comme conforme ou bien est-il significativement différent de ce que prévoit le modèle?
2. Un biologiste étudie l’envergure du Grand Rhinolophe. Dans la littérature, il trouve que l’envergure moyenne théorique µ est de 375 mm et la variance de 225 mm2.
- Dans cette population, on capture un individu dont l'envergure est de 404,5 mm. Cette envergure est-elle anormalement grande pour la population de Grand Rhinolophe (alpha = 5%) ?
- Dans cette population, on capture un individu dont l'envergure est de 409 mm. Cette envergure est-elle plus grande que celle attendue dans la population de Grand Rhinolophe (alpha = 5%) ? Qu'en est-il avec un intervalle de confiance de 99% ?
- On a capturé une chauve-souris dans un ancien clocher désaffecté. Divers paramètres ont été mesurés. Vous disposez des moyennes et des écarts-types de ces paramètres pour la population de Grands Rhinolophes. Cet individu fait-il partie de cette population ou bien appartient-il à une population de chauves-souris significativement ou très significativement plus grande? Si non, en combien de points (énoncez-les) diffère-t-il de la population de Grands Rhinolophes?
µ σ Xobservé Zobservé Z0,95 Z0,99 Conclusion Poids 26 4,5 35 Longueur oreille 23 1,5 25,2 Longueur avant-bras 57,5 1,75 58 Longueur tête-corps 64 3,5 72 Envergure 375 12,5 404,1