Intervalles de confiance
Intervalles de confiance pour l'estimation d'un paramètre de population
Pourquoi estimer des paramètres?
Dans la plupart des situations concrètes où l'application des biostatistiques est nécessaire, il est rare que les données de la population concernée par l'étude soient connues pour toute une série de raisons déjà abordées au module 10.
Précision de l'estimation : intervalle de confiance
Un paramètre estimé n'a cependant aucune valeur si la précision de l'estimation réalisée n'est pas connue. Ceci peut être réalisé:
- soit en calculant l'erreur standard;
- soit en déterminant, autour de la valeur estimée, un intervalle dont on a de bonnes raisons de croire qu'il contient la "vraie" valeur du paramètre recherché : un intervalle de confiance.
Exemple :
Imaginons que, pour une moyenne d'échantillon de 25 cm, nous calculions que son intervalle de confiance à 95% aille de 20 à 30 cm.
Cela signifie qu'il y a 95% de chance que la vraie valeur de la moyenne de la population soit comprise entre 20 et 30 cm, et que sa valeur la plus probable (sur base des données expérimentales observées) est 25 cm.
Intervalle de confiance et risque d'erreur :
Pour définir cet intervalle de confiance, nous devons d'abord déterminer quels sont les risques d'erreurs que nous pourrions accepter.
Classiquement ce risque d'erreur (alpha : α) est fixé arbitrairement et les valeurs les plus courantes sont 5%, 1% ou 0,1%.
Les confiances généralement utilisées seront donc de 1-α = 95%, 99%, ou 99,9%.
La confiance (1-α) étant centrée, l'erreur α se répartit de part et d'autre : α/2 à gauche, et α/2 à droite.
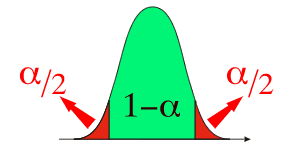
Si on reprend notre exemple précédent (Mx=25cm, intervalle de confiance à 95% qui va de 20 à 30 cm) cela signifie que nous avons encore 5% de chance que la moyenne "vraie" soit en dehors de l'intervalle 20-30 cm. Ce risque d'erreur se répartit en 2,5% de chance que la moyenne "vraie" soit inférieure à 20cm, et 2,5% de chance qu'elle soit supérieure à 30cm.
Intervalle de confiance de la moyenne lorsque la variance de la population est connue
La moyenne d'un échantillon (Mx), étant une variable aléatoire, est rarement égale à la moyenne réelle de la population (μ) dont l'échantillon est issu. Elle s'en rapproche d'autant plus que la taille de l'échantillon (n) est grande.
A partir de Mx, on peut définir un intervalle Mx ± ε (ε représentant idéalement une très petite valeur) qui a de grandes chances de contenir la moyenne réelle (μ) dela population.
La distribution d'échantillonnage de la moyenne Mx, de paramètres (μ;TeX Embedding failed!), cf. module 70, permet de délimiter autour de Mx une zone dans laquelle μ a, par exemple, 95% de chance de se trouver.
Estimation d'ε :
Lorsque la variance de la population (σ2) est connue, ε est calculé à partir de la valeur de z correspondant à la confiance utilisée: TeX Embedding failed!
avec TeX Embedding failed! la valeur de Z dont la probabilité de lui être inférieur est de TeX Embedding failed!.
Estimation de l'intervalle de confiance à 95% :
Estimation précise :
Lorsque la confiance vaut 95%, TeX Embedding failed! vaut Z0,975=1,96.
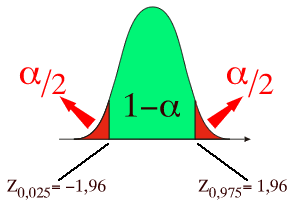
L'intervalle de confiance va donc de TeX Embedding failed! à TeX Embedding failed!
Estimation approximative :
Lorsque la confiance est de 95%, z = 1,96. On peut donc l'approximer à z=2, et considérer que l'intervalle à 95% a une longueur d'approximativement 4 fois l'erreur type de la moyenne. Dans la distribution d'échantillonnage de la moyenne, celle-ci étant centrée sur μ, la moyenne d'un échantillon a 95% de chance d'être situé dans l'intervalle μ + 2 TeX Embedding failed!.
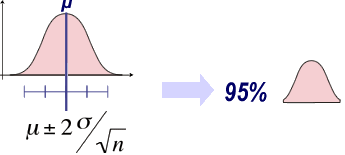
Pour un échantillon prélevé au hasard, on peut calculer l'intervalle de confiance à 95% de la moyenne. σ et n étant également connus, les limites de cet intervalle peuvent être facilement calculées :
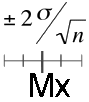
Supposons, dans la distribution tronquée, que Mx est la plus petite possible, puis qu'elle est la plus grande possible :
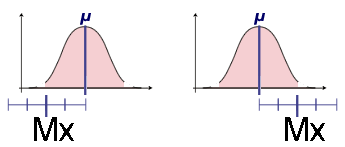
On constate que la moyenne μ se trouve toujours comprise dans l'intervalle Mx ± 2 fois l'erreur type.
La moyenne μ reste inconnue, mais elle se trouve dans des limites connues. Le risque qu'elle se trouve en dehors de ces limites est de 5% si l'intervalle de confiance a été fixé pour une confiance de 95%.
Intervalle de confiance de la moyenne lorsque la variance de la population est estimée
Lorsque la variance de la population (σ2) est inconnue, elle est estimée par celle de l'échantillon (S2), et l'erreur type de la moyenne est alors estimée par : TeX Embedding failed!.
Ceci signifie que, selon l'échantillon, la longueur de l'intervalle de confiance sera différente, car elle dépend de n (nombre d'individus dans l'échantillon) et de S (écart-type de l'échantillon).
Pour tenir compte de cette estimation de la variance, la longueur de l'intervalle de confiance est calculée à partir de la distribution de la variable t de Student.
| TeX Embedding failed! |
Si le nombre d'observations disponibles pour estimer la variance est faible, la longueur de l'intervalle de confiance à 95% sera en général beaucoup plus grande que 4 erreurs types.
Par exemple, pour n = 3, la limite supérieure est un t2; 0,975 = 4,303, la longueur de l'intervalle est donc de +/- 8 fois l'erreur type de la moyenne. Plus le nombre d'observations augmente dans l'échantillon, plus la longueur de l'intervalle de confiance se rapproche de 4 erreurs types
Pour obtenir une confiance de 99%, avec un échantillon de taille n = 3, la limite supérieure est un t2; 0,995 = 9,925. L'intervalle de confiance sera donc égal à Mx +/- 10 TeX Embedding failed!.
Exemple
Le dosage de protéines de 4 échantillons récoltés au hasard dans le stock de lait d'une laiterie donne les statistiques suivantes :
Mx=30 g/l et S2= 16 (g/l)2
La variable mesurée est supposée normale : X v.a. N ( μ,σ2 ).
Que peut-on dire de la moyenne réelle de la teneur en protéines du stock de la laiterie ?
L'expérimentateur se doute que le paramètre µ ne vaut pas exactement 30g/l. Il peut cependant affirmer que la moyenne la teneur en protéines du stock doit se trouver dans l'intervalle, la valeur de ε dépendant du niveau de confiance choisi et de l'erreur type de la moyenne :
30 ± ε
Dans notre exemple S = 4 g/l, n = 4 et la variable t a 3 degrés de liberté (d.l.). La borne supérieure de l'intervalle à 95% se trouve dans les tables : t3; 0,975 = 3,18
L'erreur type estimée = TeX Embedding failed! g/l et ε = 3,18 x 2 = 6,36 g/l.
La moyenne de la teneur en protéines du stock de la laiterie est donc comprise entre les limites 30 g/l ± 6,36 g/l soit entre 23,64 g/l et 36,36 g/l.
La confiance dans cette estimation est de 95%. Autrement dit, il y a 5% de risque que la moyenne réelle de la teneur en protéines du stock soit moins de 23,64 g/l ou plus de 36,36 g/l .
Intervalle de confiance d'une proportion
Principe général :
Le principe de l'intervalle de confiance d'un paramètre d'une population est toujours le même. La formulation générale en est :
L'intervalle de confiance = statistique de l'échantillon ± ε.
La probabilité que le paramètre de population soit situé dans cet intervalle est la confiance. ε est d'autant plus grand que la confiance souhaitée est élevée.
Cas particulier d'une proportion :
L'intervalle de confiance d'une proportion π est P ± ε avec
| TeX Embedding failed! |
Exemple :
Dans le cas d'une contamination d'un grand cheptel bovin par la bactérie Brucella abortus, un vétérinaire observe 53 avortements pour 134 vaches gestantes.
Quel risque d'avortement peut -il prédire dans le cheptel ?
Proportion : 53/134 = 0,40
Pour une confiance de 95% la borne supérieure de Z0,975 = 1,96
| TeX Embedding failed! |
Le risque d'avortement dans le cheptel a 95 chances sur 100 d'être compris entre 0,317 et 0,483.
Intervalle de confiance d'un dénombrement
Principe général :
Le principe de l'intervalle de confiance d'un paramètre d'une population est toujours le même. La formulation générale en est :
L'intervalle de confiance du paramètre = statistique de l'échantillon ± ε.
La probabilité que la paramètre de population soit réellement dans l'intervalle de confiance est la confiance. ε est d'autant plus grand que la confiance souhaitée est élevée.
Cas particulier d'un dénombrement :
L'intervalle de confiance d'un dénombrement = x ± ε (approximation d'une loi de poisson par une variable normale)
| TeX Embedding failed! |
Exemple :
Un géologue mesure une radioactivité de 150 dpm dans un prélèvement de roche. Que peut-il dire de la valeur réelle de la radioactivité ?
Exactement : la valeur de z = 1,96
| TeX Embedding failed! |
Approximativement : la valeur de Z est arrondie à 2.
| TeX Embedding failed! |
La radioactivité réelle a 95 chances sur 100 d'être comprise entre 125 et 175 dpm.
Intervalle de confiance de la pente d'une droite de régression
Dans le cadre complexe des régressions, nous n'aborderons ici que le cas particulier de la régression linéaire, dont les principes de base ont été définis dans le module 20 : Statistiques descriptives à deux dimensions. On abordera plus particulièrement le cas d'une régression à X fixé, tel que décrit dans le module 170 : Régression dans l'ANOVA 1.
Régression linéaire à X fixé :
Dans ce cas particulier, les conditions d'inférence sur la droite de régression sont strictes.
Condition 1 :
Les valeurs prises par la variable X doivent être fixées sans erreur par l'expérimentateur.
Condition 2 :
X étant une variable contrôlée (valeurs fixées par l'expérimentateur), on peut considérer Y comme fonction de X, mais pas le contraire : Y=f(X)
Condition 3:
Pour chaque valeur Xi de X, il existe une population de valeurs Yi distribuée normalement, de moyenne µi et de variance σ2 homogène c'est-à-dire constante quelle que soit la valeur de X :
Yi v.a.N(µi ;σ2 )
Condition 4:
Les moyennes µi correspondant aux valeurs Yi sont situées sur une droite dont les paramètres sont β0 et β1 telle que :
µi =β0+β1.Xi
avec β0 l'ordonnée à l'origine et β1 la pente.
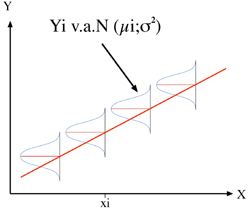
Dans ces conditions, l'intervalle de confiance de β1 = B1 ± ε avec TeX Embedding failed!
avec TeX Embedding failed!
et TeX Embedding failed!
avec :
- CMr = carré moyen résiduel
- SCEr = somme des carrés des écarts résiduels
- yo = y observé
- ym = y estimé par l'équation de la régression pour le même x que le yo
- ye = yo - ym
Exemple
Un démographe estime la croissance de la population pensionnée d'un quartier, année par année sur 5 ans :
Yo = 26%, 32%, 40%, 44%, 55% :
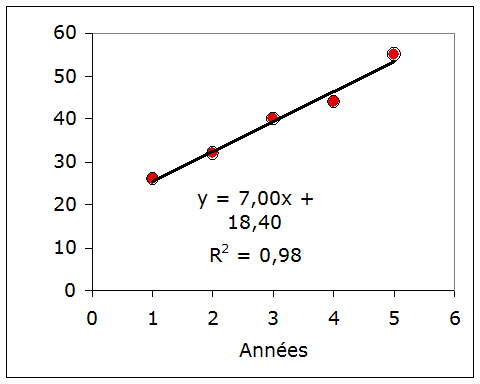
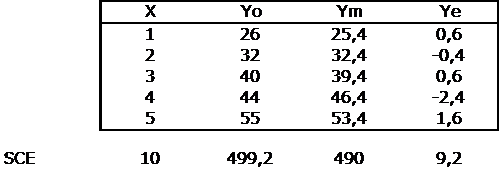
Sur base du modèle linéaire Ym = Bo + B1.X, il estime une croissance de 7,00 % par an (B1).
Tables : t3 ;0,975 = 3,18
| TeX Embedding failed! |
L'accroissement réel annuel (confiance = 95%) est donc compris entre 5,24 et 8,76%