Distribution de Chi-carré
Définition
La variable chi carré (Χ2) est une somme de variables aléatoires normales réduites au carré (une somme de z2). Sa distribution est asymétrique et dépend d'un seul paramètre k ou nombre de degrés de liberté. Ce nombre de degrés de liberté dépend du nombre de variables aléatoires normales indépendantes intervenant dans la somme.
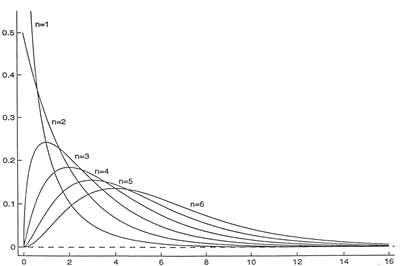
A partir de 3 degrés de liberté, les distributions Χ2 suivent une distribution en cloche caractérisée par une dissymétrie à gauche. La forme de la courbe est déterminée par le nombre de degrés de liberté. En effet, plus le nombre de degrés de liberté augmente, plus Χ2 tend vers une v.a. Normale et donc adopte une courbe en cloche.
La variable Χ2 est souvent utilisée dans les tests statistiques basés sur la somme des carrés des écarts (par exemple, somme de carrés d'écarts entre fréquences observées et fréquences théoriques).
Types de tests
Dans le cadre de ce cours de statistiques élémentaires, nous ne nous préoccuperons que de deux types de tests différents:
Utilité
La variable Chi -Carré est un modèle qui exprime la distribution de sommes de carrés d’écarts standardisés. Elle permet de calculer la probabilité d’observer des écarts dus au hasard entre des fréquences observées et celles prévues par une loi de probabilité.
Elle permet également de décrire la distribution de variances d'échantillons prélevés dans une même population.
Principe
Imaginons un modèle qui répartisse les observations en deux catégories, par exemple mâles et femelles, dans une population de sex-ratio 0,5.
| TeX Embedding failed! |
Calculons un écart quadratique entre les fréquences observées et théoriques, standardisé par la fréquence théorique : TeX Embedding failed! et rassemblons les valeurs dans un tableau :
|
mâles |
femelles |
total |
|
|
fi observée |
23 |
64 |
87 |
|
fi théorique |
29 |
58 |
87 |
|
écart quadratique standardisé |
1.24 |
0.62 |
1.86 |
Les fréquences observées fobsi correspondent approximativement à des variables aléatoires de Poisson X=Po(m), où la moyenne m est égale à n.π (π = la probabilité d’appartenir à la catégorie i) ou encore égale à la fréquence théorique fthi .
La variance attendue de cette fréquence observée est donc Var(X)= m = n.π = fthi
La quantité TeX Embedding failed! est donc approximativement une variable Z(0 ;1).
L’écart global entre les observations et le modèle est calculé par la statistique
| TeX Embedding failed! |
| TeX Embedding failed! |
Si l’on répète l’expérience un grand nombre de fois, on obtiendra différentes fréquences, et différentes valeurs de Χ2obs.
|
Echantillon N° |
mâles |
femelles |
Χ2 obs |
|
2 |
29 |
62 |
0.0879 |
|
3 |
25 |
60 |
0.5882 |
|
4 |
25 |
73 |
2.6990 |
|
5 |
32 |
63 |
0.0053 |
|
6 |
37 |
66 |
0.3107 |
|
7 |
32 |
74 |
0.4717 |
Comparons les valeurs obtenues pour Χ2 obs avec k=2 (nombre de degrés de liberté=1) :
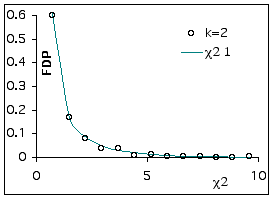
Comparaison des écarts quadratiques standardisés à la distribution théorique de khi-carré avec un degré de liberté.
Exemple
Imaginons un modèle qui répartisse les observations en trois catégories, par exemple les produits AA, Aa et aa de plusieurs croisements hétérozygotes, de probabilité 25%, 50% et 25% respectivement. Effectuons 5 fois l’expérience qui consiste à relever la fréquence de chaque phénotype :
|
N° |
AA |
Aa |
aa |
Χ2obs |
|
1 |
27 |
49 |
20 |
|
|
2 |
17 |
53 |
31 |
4.13 |
|
3 |
27 |
46 |
22 |
0.62 |
|
4 |
22 |
46 |
27 |
0.62 |
|
5 |
28 |
53 |
17 |
3.12 |
Comment sont calculées ces valeurs ?
Ligne 1: 27+49+20=96 données, ce qui donne des fréquences théoriques de 24, 48, et 24 (25%, 50%, 25% de 96).
Le Chi²observé est donc TeX Embedding failed!, c'est à dire 1.06 si on arrondit à deux chiffres significatifs.
Répétition de l’expérience, fréquences observées et valeurs de Chi²observé
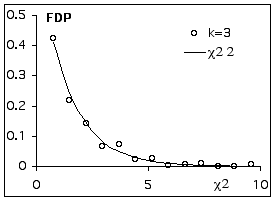
Comparaison des écarts quadratiques standardisés à la distribution théorique de Chi² avec deux degrés de liberté.
Considérons la probabilité a priori de 10 acides aminés de se trouver dans une hélice alpha et dénombrons leur fréquence dans 4 protéines.
|
Acide aminé |
Probabilité |
Protéines |
|||
|
1 |
2 |
3 |
4 |
||
|
Ile |
0.03 |
4 |
3 |
3 |
3 |
|
Asn |
0.05 |
8 |
5 |
8 |
4 |
|
Val |
0.07 |
12 |
7 |
8 |
4 |
|
Thr |
0.07 |
5 |
8 |
7 |
9 |
|
Tyr |
0.07 |
9 |
7 |
10 |
5 |
|
Leu |
0.13 |
8 |
15 |
15 |
12 |
|
Pro |
0.13 |
14 |
13 |
12 |
13 |
|
Glu |
0.15 |
9 |
18 |
16 |
17 |
|
Gly |
0.15 |
17 |
12 |
16 |
10 |
|
Met |
0.15 |
12 |
16 |
18 |
20 |
|
total |
1 |
98 |
104 |
113 |
97 |
|
Χ2obs |
12.32 |
1.49 |
2.35 |
6.40 |
|
Probabilités, fréquences observées et Chi² observé pour 10 acides aminés répertoriés dans les hélices alpha de 4 protéines.
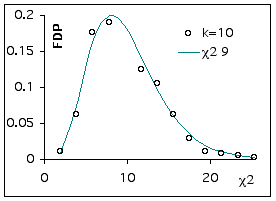
Si l’on répète l’expérience sur un plus grand nombre de protéines, on observe une distribution de Chi²observé qui peut se comparer à une distribution théorique de Chi² avec 9 degrés de liberté.
Tables de Chi-carré
La distribution de Χ2 est utilisée pour tester des statistiques basées sur le calcul de la somme des carrés des écarts
Les degrés de liberté déterminent la forme de la courbe et dépendent du nombre de catégories dans lesquelles les fréquences sont dénombrées.
Plus le nombre de degrés de liberté augmente, plus Χ2 tend vers une v.a. Normale.
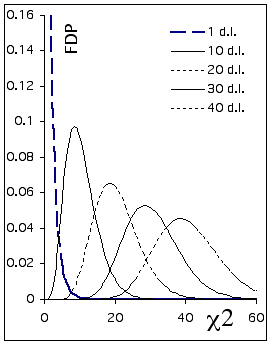
Figure - Comparaison de fonctions Χ2 avec différents nombres de degrés de liberté. La distribution de Χ2 avec un petit nombre de degrés de liberté est fortement asymétrique.
La table de Χ2 est généralement présentée de la façon suivante :
|
0.9 |
0.95 |
0.975 |
0.99 |
|
|
1 |
2.71 |
3.84 |
5.02 |
6.63 |
|
2 |
4.61 |
5.99 |
7.38 |
9.21 |
|
3 |
6.25 |
7.81 |
9.35 |
11.34 |
|
4 |
7.78 |
9.50 |
11.14 |
13.28 |
La première ligne énumère des probabilités, la première colonne, le nombre de degrés de liberté. Chaque cellule comprend la valeur de Χ2 telle que P[Χ2 < Χ2dl]=p , p étant la probabilité reprise en tête de colonne et dl le nombre de degrés de liberté repris en tête de ligne.
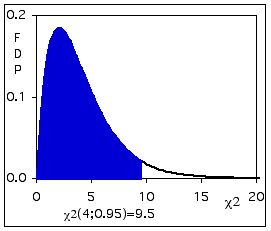
Figure - Illustration de la probabilité reprise dans la table, 4 d.l. p= 0.95.
Chi-carré et MS Excel
Dans le tableur Excel, la fonction LOI.KHIDEUX(x;dl) renvoie la probabilité TeX Embedding failed! avec dl= nombre de degrés de liberté.
Dans notre exemple, LOI.KHIDEUX(9,5 ;4) renvoie 0,95.
Cette formule est aussi valide si vous utilisez OpenOffice Calc.
Attention: les conventions d’Excel varient d’une fonction de probabilité à l’autre.