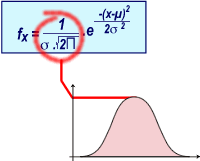
Distributions aléatoires continues
Distribution Normale
Généralités
La variable aléatoire normale est une variable continue dont la distribution est symétrique et suit une courbe de Gauss-Laplace. Beaucoup de variables biologiques suivent une loi normale.
Exemple: si l'on s'intéresse à la taille de chauves-souris, les individus peut être rangés dans des classes de tailles d'intervalles constants comme décrit précédemment dans les statistiques descriptives à une dimension. Si la population est composée d'un grand nombre d'individus, on peut les classer dans une infinité de classes d'intervalles Li tendant vers 0. L'histogramme est alors remplacé par une courbe de Gauss-Laplace:

Pour des échantillons de taille finie, l'ordonnée de l'histogramme se représente par des densités de fréquences relatives alors que pour la population on parle de densités de probabilités (n tend vers l'infini et delta x tend vers 0)
Propriétés
Equation et symbolique
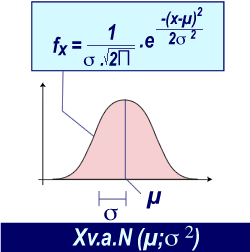
La fonction de densité de probabilités (fx) se caractérise par une équation faisant intervenir la moyenne µ et la variance σ2. Par convention, nous adopterons la convention d'écriture: X v.a.N(µ;σ2) . Dans la littérature, on peut aussi trouver: µ±σ (moyenne ± écart-type).
Symétrie autour de la moyenne
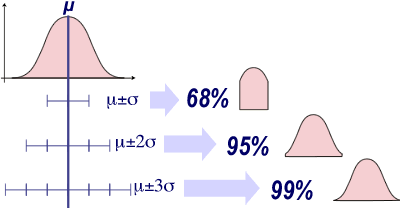
La courbe de Gauss-Laplace est symétrique:
- Lorsqu'on sélectionne l'intervalle compris entre +1 et -1 écart-type autour de la moyenne µ (de μ-σ jusque μ+σ), on isole 68% des individus d'une population normale.
- Lorsqu'on sélectionne l'intervalle compris entre +2 et -2 écarts-types autour de la moyenne µ (de μ-2σ jusque μ+2σ), on isole 95% des individus d'une population normale.
- Lorsqu'on sélectionne l'intervalle compris entre +3 et -3 écarts-types autour de la moyenne µ (de μ-3σ jusque μ+3σ), on isole 99% des individus d'une population normale.
Modification de la variance
Lorsque la variance d'une population diminue, cela se traduit par une dispersion moins importante de la courbe autour de la moyenne. Parallèlement, le sommet de la courbe tend à s'élever afin de préserver une surface totale sous la courbe égale à 1 (ou 100%).
Exemple:
Dans une population de chauves-souris de l'espèce A, l'envergure X est une v.a. N(375; 225)
Dans une population de chauves-souris de l'espèce A femelles, l'envergure X est une v.a. N(375; 121)
Dans une population de chauves-souris de l'espèce A femelles de 3 mois, l'envergure X est une v.a. N(375; 49)
etc.
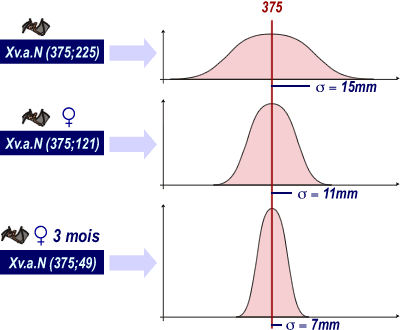
Influence de la variance sur le sommet de la courbe de Gauss:
Si la variance diminue, le sommet de la courbe tend à augmenter.
En effet, dans l'équation de la courbe, l'écart-type se trouve au dénominateur (voir terme entouré en rouge). Plus l'écart-type est petit, plus ce terme tend à devenir grand.
Réduction de variable
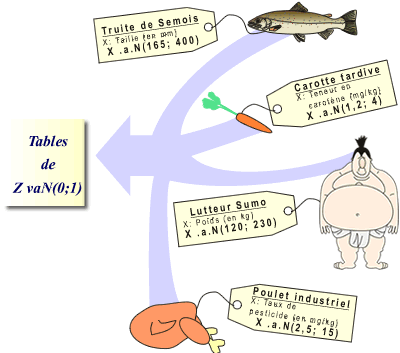
Chaque v.a. normale possède sa propre moyenne (µ) et variance (σ2). Déterminer des probabilités sous ce type de courbe de Gauss (à chaque cas particulier est associée une courbe de moyenne et de variance particulière) requiert un algorithme d'intégration numérique.
Heureusement, toutes les v.a. Normales peuvent se réduire à une seule et même distribution normale réduite Z. La distribution réduite de Z est centrée sur une moyenne 0 et possède une variance 1. La table de probabilité de Z a été calculée une fois pour toutes et dispense des probabilités du type:
P(Z ≤zi)
Comment réduire?
Toute v.a. normale peut être ramenée à une variable normale réduite Z v.a. N (0;1) par simple transformation algébrique (soustraction de la moyenne et division par l'écart-type). Cette opération est appelée réduction de la variable étudiée X en la variable réduite Z.
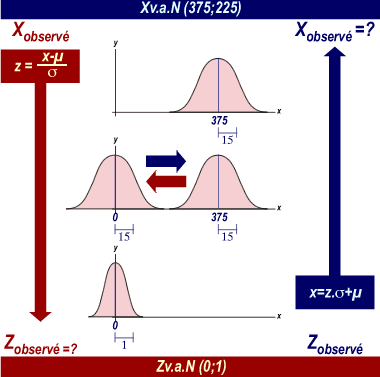
Convertir une valeur expérimentale (Xobservé) en une valeur réduite (Zobservé)
Xobservé = 390 et X v.a.N (375;225), alors TeX Embedding failed!
Convertir une valeur réduite (Zobservé) en une valeur expérimentale (Xobservé)
Zobservé = 2,5 et X v.a.N (375;225), alors TeX Embedding failed!
Théorème central limite
Le théorème central limite est un théorème mathématique qui définit les paramètres de la distribution d'échantillonnage, ou distribution des moyennes des échantillons en fonction des paramètres de la population de départ et la taille de d'échantillon.
Selon le théorème central limite, les moyennes des échantillons indépendants provenant d'une même population (µ;σ²) se distribuent selon une distribution normale de paramètres (TeX Embedding failed!).
Illustration avec une variable aléatoire normale
Soient x1, x2, x3 ... x∞ les tailles (cm) de truites arc-en-ciel. La taille de ces truites se distribue selon une distribution normale de paramètres :
X v.a. N(µ;σ²)
Si on prélève des échantillons indépendants (les poissons sont choisis au hasard) de n individus, toutes les moyennes de ces échantillons se distribuent selon une loi normale de même moyenne, mais de variance plus faible, avec TeX Embedding failed!.
La racine carrée de TeX Embedding failed! est appelée l'erreur standard de la moyenne (SEM ou standard error of the mean) ou encore écart-type de la moyenne.
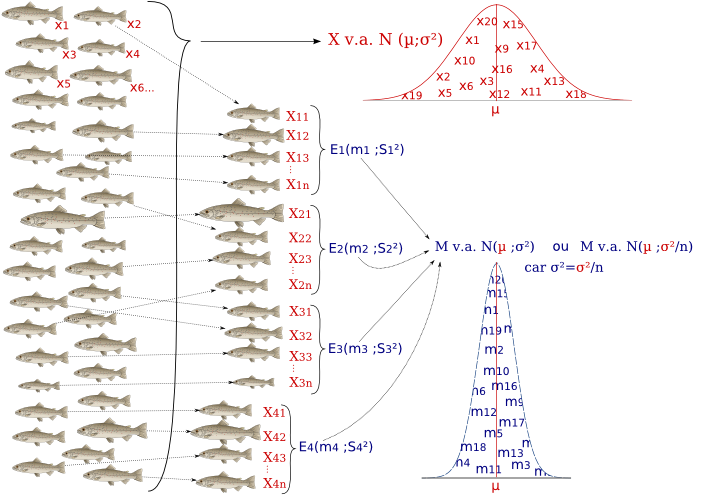
Exemples :
Si les truites proviennent d'une population normale de paramètres (15;4), les échantillons de 4 truites auront des moyennes qui se distribuent selon une loi normale de paramètres (15;1).
Si les truites proviennent d'une population normale de paramètres (20;12), les échantillons de 3 truites auront des moyennes qui se distribuent selon une loi normale de paramètres (20;4).
etc...
Illustration avec une variable Binomiale
Le théorème central limite s'applique aussi aux distributions discontinues telles que les distributions Binomiales ou de Poisson.
Prenons le cas du lancer d'un dé. Si le dé a 6 faces, et qu'il est équilibré, chaque face a 1/6ème de chance d'être affichée lors d'un lancer.
Si je lance le dé une seule fois, P(face=1)=P(face=3)=1/6
Si je lance le dé 10 fois P(moyenne=1)<P(moyenne=3)
Si je lance le dé 100 fois P(moyenne=1)<<<<<<P(moyenne=3)
etc...
Même si la variable est discontinue, la distribution des valeurs des moyennes des échantillons tend à suivre une loi normale de paramètres (µ;σ²/n) avec µ=moyenne de la population des valeurs de départ, et σ² la variance de cette population de départ, pour autant que la taille n de l'échantillon soit suffisamment grande.
Conséquence du théorème central limite
Lorsqu'on dispose des données de population (µ;σ²) et qu'on vous demande de calculer des probabilités associées à des valeurs moyennes réalisées sur n mesures, vous devez replacer ces valeurs moyennes dans leur distribution (TeX Embedding failed!) et non pas dans la distribution des valeurs des individus (µ;σ²).
Utilisation des tables de Z et de T de Student
Utilisation de la table de Z:
La table de Z (accessible depuis le lien "Tables" en haut de toutes les pages de ce site) vous donne les probabilités associées à des valeurs de z selon la relation p(Z<z).
Exemple : quelle est la probabilité d'avoir une valeur inférieure à 1,96 dans une distribution de Z v.a. N(0;1) ?
La table vous donne la réponse :
En tête de ligne on trouve la valeur entière et la première décimale de la valeur z.
En tête de colonne on trouve la seconde décimale de z.
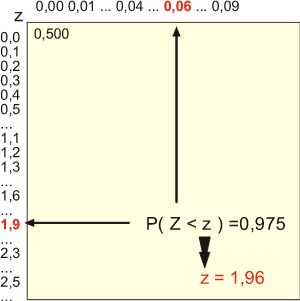
Donc P(Z<1,96)=0,975=97,5%
Inconvénient de la table de Z :
On peut lire la table à l'envers, donc par déduction, on peut y trouver les valeurs de Z qui correspondent à une certaine probabilité.
Cependant toutes les probabilités intéressantes ne sont pas forcément représentées.
Si, par exemple, on cherche le z en dessous duquel il y a 98,5% des individus, on cherche la valeur 0,985 dans les valeurs du tableau, et en regardant les en-têtes de ligne et de colonne je trouve que le z qui correspond est 2,17 (ligne 2,1 et colonne 0,07).
Mais si je cherche le z tel que P(Z<z)=0,8=80%, il n'y a pas 0,8 dans les valeurs. On passe de 0,79955 à 0,80234, donc le z tel que P(Z<z)=0,8 est compris entre 0,84 et 0,85.
Cette table peut donc s'employer dans le sens :
z connu --> trouver la probabilité P(Z ≤ z)
ou dans le sens :
probabilité P(Z ≤ z) connue--> trouver le z correspondant, mais elle n'est pas toujours pratique dans ce sens là.
Utilisation de la table de Student :
La table de Student, telle que présentée dans ce site, part des probabilités et donne les valeurs des variables correspondantes de t selon le nombre de degrés de liberté de la variable t (en-tête de ligne).
Si la variance de la population est connue (σ2), on peut employer la table de t de Student pour retrouver la valeur de z en considérant qu' il s'agit d'une variable t où le nombre de dégrés de liberté est infini (dernière ligne).
L'avantage d'une telle table est de pouvoir donner rapidement des valeurs de Z pour des probabilités très couramment utilisées dans les tests d'hypothèses.
- En tête de colonne (p): donne la probabilité P(Z ≤ z)
- En tête de ligne (k): se positionner en l'"infini"
Dans notre exemple précédent :
P(Z<z)=0,8=80% donne ici directement une valeur exacte de 0,842.
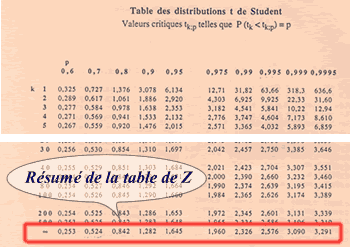
En conclusion
Pour trouver une probabilité à partir d'une valeur de z : on utilise la table de Z.
Pour trouver une valeur de z à partir d'une probabilité fixée : on utilise la table de student, dernière ligne.
Exercices
Une vache produit quotidiennement 36 ± 5 litres de lait.
- Définissez la variable étudiée et ses paramètres.
- Quelle est la probabilité qu'une vache prise au hasard ait une production laitière inférieure à 30 l/jour ?
-
Quelle est la probabilité que la production laitière soit comprise entre :
- la moyenne plus ou moins 1 écart-type ?
- la moyenne plus ou moins 2 écarts-types ?
- La population comprend 5 % de vaches considérées comme étant des mauvaises productrices (faible production laitière), et 5 % de vaches considérées comme étant des excellentes productrices (production laitière élevée). Le reste de la population est considéré comme peuplé de vaches à production correcte. A partir de quelle production journalière peut-on considérer qu'une vache est mauvaise productrice ou excellente productrice ?
- Quelle est la probabilité qu'une productrice correcte produise moins de 36 l/jour ?
- Quelle est la probabilité qu'une productrice correcte ait une production inférieure à 30 l/jour ?
- Quelle est la probabilité qu'une vache ayant une production inférieure à 30 l/jour soit une productrice correcte ?
- Quelle est la probabilité qu'une vache prise au hasard soit une productrice laitière correcte et ai une production supérieure à 36 l/jour ?
Pour répondre vous devez consulter les tables.
Distribution de Student
Définition et conditions d'application
La variable alétoire t de Student est une variable aléatoire continue dont la fonction de densité de probabilités est symétrique et dépend d'un paramètre k ou nombre de degrés de liberté. Elle est obtenue par réduction d'une variable aléatoire normale (comme la variable Z abordée au module 70) mais la variance de la population σ2 est remplacée par la variance S2 de l'échantillon. Le nombre de degrés de liberté k est en général, égal à la taille de l'échantillon n -1.
| TeX Embedding failed! |
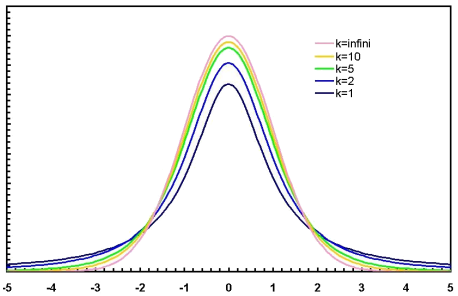
D'après Thorin sur fr.wikipedia.org
Comme la variable réduite Z (voir module 70), la variable t de Student a pour moyenne 0, mais sa variance n'est plus 1, elle est toujours > 1, mais d'autant plus proche de 1 que son nombre de degrés de liberté est grand. Lorsque n = ∞, t v.a. N(0;1). Donc, lorsque n = ∞ -> t=z.
La réduction de Student est communément employée pour convertir une moyenne expérimentale en une valeur réduite selon l'application du Théorème central limite (voir ces quelques pages...).
La réduction d'une variable observée, ici la moyenne d'un échantillon, en une variable t s'effectue comme suit:
Au lieu de :
| TeX Embedding failed! |
| TeX Embedding failed! |
Cette valeur de t observée tient compte de la taille de l'échantillon, car plus n est grand, plus S estime correctement σ. La précision de cette estimation est prise en compte dans le modèle mathématique de la distribution de Student à travers le nombre de degrés de liberté (k=n-1), qui augmente d'autant plus que n augmente.
Exemple :
Cherchons dans les tables la valeur réduite en dessous de laquelle on trouve 95% des individus :
Dans le cas de z v.a. N(0;1) si P(Z<z)=0,95 -> z=1,645
Dans le cas d'une distribution de Student avec k=40 degrés de liberté : t40;0,95 = 1,684
Dans le cas d'une distribution de Student avec k=20 degrés de liberté : t20;0,95 = 1,725
Dans le cas d'une distribution de Student avec k=10 degrés de liberté : t10;0,95 = 1,812
Dans le cas d'une distribution de Student avec k=5 degrés de liberté : t5;0,95 = 2,015
...
Exercices
1. Soit une population de chauves-souris dont on connait la longueur moyenne des oreilles (µ=23 mm). On prélève un échantillon de 21 chauves-souris dont la longueur moyenne des oreilles est de 22,34 mm avec une variance de 49 mm2. La moyenne de cet échantillon se situe-t-elle dans les 95% des moyennes les plus plausibles autour de la moyenne de la population ?
2. Soit une population de chauves-souris dont on connait la longueur moyenne des oreilles (µ=23 mm). On prélève un échantillon de 21 chauves-souris dont la longueur moyenne des oreilles est de 20,5 mm avec une variance de 16 mm2. La moyenne de cet échantillon se situe-t-elle dans les 95% des moyennes les plus plausibles autour de la moyenne de la population ?
3. Pour une population de vipères à collier adultes, on enregistre une longueur moyenne de corps de 130 cm. Sachant qu'on prélève un échantillon de 9 individus dont la longueur moyenne est de 133,33 cm avec une variance de 81 cm2.
- La moyenne de cet échantillon se situe-t-elle dans les 95% des moyennes les plus plausibles autour de la moyenne de la population ?
- Qu'en est-il avec un autre échantillon de 9 individus dont la moyenne vaut 139 cm et de même variance que le précédent ?
Distribution de Chi-carré
Définition
La variable chi carré (Χ2) est une somme de variables aléatoires normales réduites au carré (une somme de z2). Sa distribution est asymétrique et dépend d'un seul paramètre k ou nombre de degrés de liberté. Ce nombre de degrés de liberté dépend du nombre de variables aléatoires normales indépendantes intervenant dans la somme.
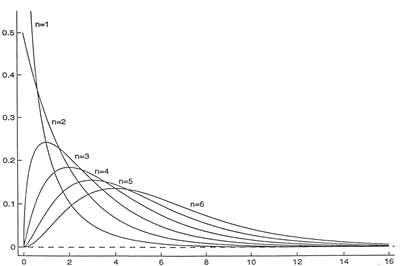
A partir de 3 degrés de liberté, les distributions Χ2 suivent une distribution en cloche caractérisée par une dissymétrie à gauche. La forme de la courbe est déterminée par le nombre de degrés de liberté. En effet, plus le nombre de degrés de liberté augmente, plus Χ2 tend vers une v.a. Normale et donc adopte une courbe en cloche.
La variable Χ2 est souvent utilisée dans les tests statistiques basés sur la somme des carrés des écarts (par exemple, somme de carrés d'écarts entre fréquences observées et fréquences théoriques).
Types de tests
Dans le cadre de ce cours de statistiques élémentaires, nous ne nous préoccuperons que de deux types de tests différents:
Utilité
La variable Chi -Carré est un modèle qui exprime la distribution de sommes de carrés d’écarts standardisés. Elle permet de calculer la probabilité d’observer des écarts dus au hasard entre des fréquences observées et celles prévues par une loi de probabilité.
Elle permet également de décrire la distribution de variances d'échantillons prélevés dans une même population.
Principe
Imaginons un modèle qui répartisse les observations en deux catégories, par exemple mâles et femelles, dans une population de sex-ratio 0,5.
| TeX Embedding failed! |
Calculons un écart quadratique entre les fréquences observées et théoriques, standardisé par la fréquence théorique : TeX Embedding failed! et rassemblons les valeurs dans un tableau :
|
mâles |
femelles |
total |
|
|
fi observée |
23 |
64 |
87 |
|
fi théorique |
29 |
58 |
87 |
|
écart quadratique standardisé |
1.24 |
0.62 |
1.86 |
Les fréquences observées fobsi correspondent approximativement à des variables aléatoires de Poisson X=Po(m), où la moyenne m est égale à n.π (π = la probabilité d’appartenir à la catégorie i) ou encore égale à la fréquence théorique fthi .
La variance attendue de cette fréquence observée est donc Var(X)= m = n.π = fthi
La quantité TeX Embedding failed! est donc approximativement une variable Z(0 ;1).
L’écart global entre les observations et le modèle est calculé par la statistique
| TeX Embedding failed! |
| TeX Embedding failed! |
Si l’on répète l’expérience un grand nombre de fois, on obtiendra différentes fréquences, et différentes valeurs de Χ2obs.
|
Echantillon N° |
mâles |
femelles |
Χ2 obs |
|
2 |
29 |
62 |
0.0879 |
|
3 |
25 |
60 |
0.5882 |
|
4 |
25 |
73 |
2.6990 |
|
5 |
32 |
63 |
0.0053 |
|
6 |
37 |
66 |
0.3107 |
|
7 |
32 |
74 |
0.4717 |
Comparons les valeurs obtenues pour Χ2 obs avec k=2 (nombre de degrés de liberté=1) :
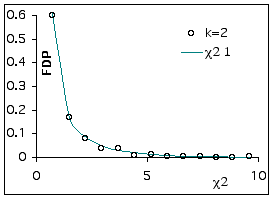
Comparaison des écarts quadratiques standardisés à la distribution théorique de khi-carré avec un degré de liberté.
Exemple
Imaginons un modèle qui répartisse les observations en trois catégories, par exemple les produits AA, Aa et aa de plusieurs croisements hétérozygotes, de probabilité 25%, 50% et 25% respectivement. Effectuons 5 fois l’expérience qui consiste à relever la fréquence de chaque phénotype :
|
N° |
AA |
Aa |
aa |
Χ2obs |
|
1 |
27 |
49 |
20 |
|
|
2 |
17 |
53 |
31 |
4.13 |
|
3 |
27 |
46 |
22 |
0.62 |
|
4 |
22 |
46 |
27 |
0.62 |
|
5 |
28 |
53 |
17 |
3.12 |
Comment sont calculées ces valeurs ?
Ligne 1: 27+49+20=96 données, ce qui donne des fréquences théoriques de 24, 48, et 24 (25%, 50%, 25% de 96).
Le Chi²observé est donc TeX Embedding failed!, c'est à dire 1.06 si on arrondit à deux chiffres significatifs.
Répétition de l’expérience, fréquences observées et valeurs de Chi²observé
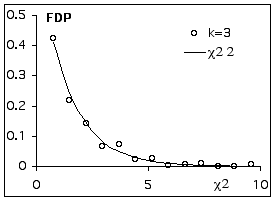
Comparaison des écarts quadratiques standardisés à la distribution théorique de Chi² avec deux degrés de liberté.
Considérons la probabilité a priori de 10 acides aminés de se trouver dans une hélice alpha et dénombrons leur fréquence dans 4 protéines.
|
Acide aminé |
Probabilité |
Protéines |
|||
|
1 |
2 |
3 |
4 |
||
|
Ile |
0.03 |
4 |
3 |
3 |
3 |
|
Asn |
0.05 |
8 |
5 |
8 |
4 |
|
Val |
0.07 |
12 |
7 |
8 |
4 |
|
Thr |
0.07 |
5 |
8 |
7 |
9 |
|
Tyr |
0.07 |
9 |
7 |
10 |
5 |
|
Leu |
0.13 |
8 |
15 |
15 |
12 |
|
Pro |
0.13 |
14 |
13 |
12 |
13 |
|
Glu |
0.15 |
9 |
18 |
16 |
17 |
|
Gly |
0.15 |
17 |
12 |
16 |
10 |
|
Met |
0.15 |
12 |
16 |
18 |
20 |
|
total |
1 |
98 |
104 |
113 |
97 |
|
Χ2obs |
12.32 |
1.49 |
2.35 |
6.40 |
|
Probabilités, fréquences observées et Chi² observé pour 10 acides aminés répertoriés dans les hélices alpha de 4 protéines.
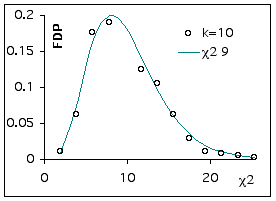
Si l’on répète l’expérience sur un plus grand nombre de protéines, on observe une distribution de Chi²observé qui peut se comparer à une distribution théorique de Chi² avec 9 degrés de liberté.
Tables de Chi-carré
La distribution de Χ2 est utilisée pour tester des statistiques basées sur le calcul de la somme des carrés des écarts
Les degrés de liberté déterminent la forme de la courbe et dépendent du nombre de catégories dans lesquelles les fréquences sont dénombrées.
Plus le nombre de degrés de liberté augmente, plus Χ2 tend vers une v.a. Normale.
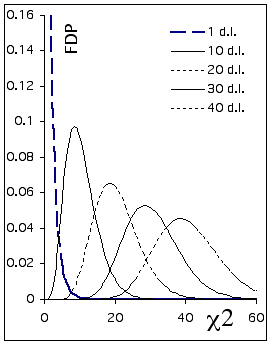
Figure - Comparaison de fonctions Χ2 avec différents nombres de degrés de liberté. La distribution de Χ2 avec un petit nombre de degrés de liberté est fortement asymétrique.
La table de Χ2 est généralement présentée de la façon suivante :
|
0.9 |
0.95 |
0.975 |
0.99 |
|
|
1 |
2.71 |
3.84 |
5.02 |
6.63 |
|
2 |
4.61 |
5.99 |
7.38 |
9.21 |
|
3 |
6.25 |
7.81 |
9.35 |
11.34 |
|
4 |
7.78 |
9.50 |
11.14 |
13.28 |
La première ligne énumère des probabilités, la première colonne, le nombre de degrés de liberté. Chaque cellule comprend la valeur de Χ2 telle que P[Χ2 < Χ2dl]=p , p étant la probabilité reprise en tête de colonne et dl le nombre de degrés de liberté repris en tête de ligne.
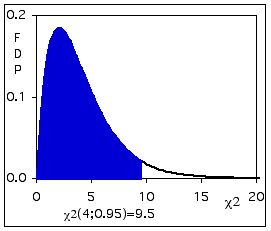
Figure - Illustration de la probabilité reprise dans la table, 4 d.l. p= 0.95.
Chi-carré et MS Excel
Dans le tableur Excel, la fonction LOI.KHIDEUX(x;dl) renvoie la probabilité TeX Embedding failed! avec dl= nombre de degrés de liberté.
Dans notre exemple, LOI.KHIDEUX(9,5 ;4) renvoie 0,95.
Cette formule est aussi valide si vous utilisez OpenOffice Calc.
Attention: les conventions d’Excel varient d’une fonction de probabilité à l’autre.
Distribution de Fisher-Snedecor
Définition et utilité
La distribution F de Fisher-Snedecor est souvent utilisée pour comparer deux variances. On peut montrer que le rapport de deux variances suit une loi de Fisher caractérisée par deux nombres de degrés de liberté (k et r) correspondant au nombre de degrés de liberté du numérateur et au nombre de degrés de liberté du dénominateur. La variable F ne peut prendre que des valeurs positives et sa distribution est fortement asymétrique.
Exemple: Test de comparaison de 2 variances
Ce test a pour objectif de vérifier si les variances de deux populations sont différentes ou non à partir des variances S²1 et S²2, calculées à partir des échantillons de tailles respectives n1 et n2, prélévés dans les 2 populations.
H0: σ²1 = σ²2
H1: σ²1 différent de σ²2
Supposons que S²1 soit plus grande que S²2
La statistique à utiliser pour éprouver H0 est: TeX Embedding failed!
Il s'agit d'une variable aléatoire F de Fisher-Snedecor à k et r degrés de liberté où: k = (n1-1) degrés de liberté Pour faciliter la lecture des tables la variance la plus grande se placera au numérateur et le seuil de confiance (1-α) sera (1-TeX Embedding failed!) La conclusion du test est: si Fobs est plus grand que le F théorique (avec k et r degrés de liberté et la probabilité 1-TeX Embedding failed!), alors il y aura rejet de l'hypothèse nulle (H0): le rapport entre les 2 variances observées est trop grand pour être attribué au hasard de l'échantillonnage.
r = (n2-1) degrés de liberté
Choisir la page de F en fonction de p=... (0,95; 0,975; 0,99; etc.)
k
r
1
2
3
4
5
...
...
...
1
2
P(Fk;r<Fk;r;p)=p
3
...
...
...
...
Comparaison de variances
La variable aléatoire F de Fisher est souvent utilisée pour comparer les variances de deux échantillons de tailles différentes. L'homogénéité des variances des populations (homoscedasticité) est une condition prélable à la comparaison des moyennes des populations. Si les variances sont hétérogènes, on ne peut comparer les moyennes. Une solution parfois possible est de transformer les données (par exemple X'= log(x)), ce qui pourrait rendre les variances plus homogènes.
Dans le cas où l'expérience contient plus de deux échantillons, on emploiera le test de Hartley, pour autant que les échantillons soient de même taille.
Le rapport de deux variances (carrés moyens) calculé dans une analyse de variance (ANOVA) se teste également par une variable de Fisher. Par exemple:
| TeX Embedding failed! |
Qui est aussi une valeur F de Fisher-Snedecor pour k et r degrés de liberté tels que:
- k = nombre de degrés de liberté du niveau expliqué analysé (na-1 avec na le nombre d'échantillons comparés)
- r = N-na (avec N le nombre total d'individus de l'expérience et na le nombre d'échantillons comparés)
Comme précédemment, si le Fobs est supérieur au F théorique, il y a RH0.