Les variables aléatoires discrètes et continues

Il existe deux grands types de variables aléatoires: les variables discontinues (ou discrètes) et les variables continues.

Les variables aléatoires discrètes

Nous envisageons des variables aléatoires discrètes (X) qui ne peuvent prendre que des valeurs entières positives ou nulles. La distribution des ces variables se représente par un diagramme en barres avec, en abscisse, les valeurs individuelles x_i et, en ordonnée, la probabilité. Pour un échantillon de données, la probabilité sera estimée par la fréquence relative.

Exemple: les distributions binomiales et de Poisson.

Les variables aléatoires continues

Nous envisageons des variables aléatoires continues (X) qui peuvent prendre n'importe quelles valeurs entre deux bornes, éventuellement entre + ou - l'infini. Comme il existe une infinité de valeurs entre deux valeurs x et x+Δ_x (Δ_x tendant vers 0), la probabilité que la variable prenne la valeur exacte x_i est nulle: P(X=x_i)=0.

La distribution des ces variables continues se représente par une fonction continue ou densité de probabilité en fonction des valeurs de la variable. Dans le cas d'un échantillon, la distribution sera représentée par un histogramme avec, en abscisse, les classes de valeurs et, en ordonnée, la fréquence relative ou la densité de fréquences relative (féquence relative divisée par l'intervalle de classe).

Pour établir un histogramme, les valeurs x_i doivent être regroupées en classes.

La variable X est représentée en abscisse. En ordonnée, on représente la densité de fréquences relatives ou, pour n tendant vers l'infini, la densité de probabilités.

Exemple: Parmi ces distributions figurent les distributions normales, normales réduites, t de Student, chi-carré et F de Fisher-Snedecor.

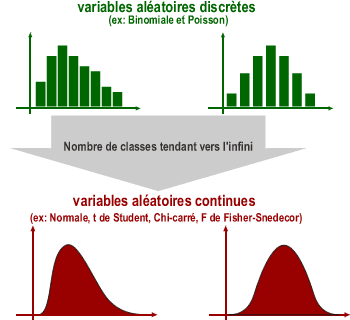
Approximer une variable aléatoire discrète par une variable aléatoire normale

Les distributions des variables aléatoires discrètes binomiales et de Poisson se représentent par des diagrammes de barres et s’emploient dans les conditions particulières suivantes :

• La variable aléatoire binomiale représente le nombre de succès parmi n épreuves élémentaires. Pour chaque épreuve, on a une probabilité constante de succès π (probabilité d'échec=1-π) (voir aussi le module v.a. binomiale) et les n épreuves sont indépendantes.
• La variable aléatoire de Poisson recense le nombre de réalisations d'un événement par unité de temps, de surface, de volume, etc. (voir aussi le module v.a. de Poisson)

Les distributions des ces 2 variables tendent vers une distribution aléatoire normale dans certaines conditions :
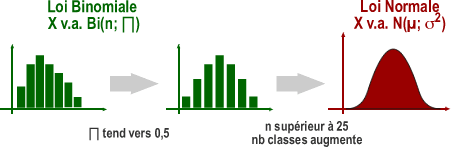
X v.a. Bi (n;π) avec n supérieur à 25 et π proche de 0,5 peut être approximée par une variable aléatoire normale avec moyenne =n.π et variance=n.π(1-π)

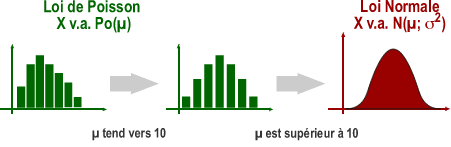
X v.a. Po (µ) avec µ supérieur à 10 peut être approximée par une variable aléatoire normale avec moyenne et variance = µ

Distributions continues: la variable aléatoire normale (X) et la variable aléatoire normale réduite (Z)

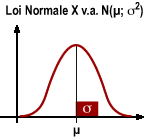
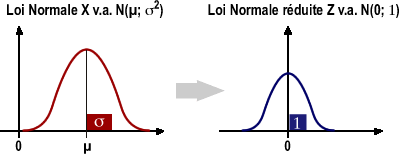
La loi normale caractérise les variables continues dont la fonction de densité de probabilité suit une courbe de Gauss-Laplace : elle est notée X v.a. N (µ ; σ²). La fonction de densité de probabilité dépend de 2 paramètres: la moyenne µ et la variance σ², qui sont propres à chaque variable. Calculer la probabilité que X soit inférieure à une valeur x revient à intégrer la fonction de densité de probabilité jusqu'à la valeur x. Beaucoup de variables biologiques obéissent à un tel modèle.

Toute variable aléatoire normale moyenne µ et la variance σ² peut se ramener, par simple transformation algébrique, à une variable aléatoire normale centrée sur 0 et de variance 1 : c’est la variable aléatoire réduite Z [ Z v.a. N (0 ;1)]. La conversion se fait par l’intermédiaire de la formule suivante :

L'avantage de la distribution normale réduite est qu'elle est unique et qu'il existe une seule table donnant les probabilités pour un grand nombre de valeurs de Z. Calculer la probabilité que P[X<x] revient à calculer la P[Z<z] avec TeX Embedding failed!

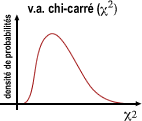
Distributions continues asymétriques (Chi-carré et F de Fisher)

La variable Chi-carré est une somme de variables aléatoires normales réduites au carré (une somme de z²). Sa distribution est asymétrique et dépend d'un seul paramètre k ou nombre de degrés de liberté. Ce nombre de degrés de liberté dépend du nombre de variables aléatoires normales indépendantes intervenant dans la somme.

Exemple : dans certains contextes expérimentaux, l’expérimentateur est amené à comparer des fréquences observées (fobs) à des fréquences prédites par un modèle (fth). Pour chaque catégorie (classe), il est possible de calculer des différences observées réduites au carré (Chi-carré).

Comparons la formule de z et de chi carré: TeX Embedding failed! et TeX Embedding failed! basée sur la propriété que, pour une variable aléatoire de Poisson,  la moyenne m est égale à la variance σ² et qu'ils sont tous deux estimés par fth. La valeur chi carré observée doit donc être comparée à une distribution Chi-carré avec k degrés de liberté (= nombre de classes moins 1).

Exercices

Exercice 1

Une étude est réalisée sur une population de chauve-souris. L’envergure moyenne est, selon des publications très sérieuses, de (375 ± 15) millimètres.

1. De quel type de variable aléatoire parle-t-on ? Définissez-la en employant la symbolique vue au cours
2. Quel modèle doit-on associer à cette variable aléatoire ? Aidez-vous du formulaire pour écrire l’équation de ce modèle. Que vaut la densité de probabilité au sommet de la fonction de probabilité du modèle f(x) ?
3. Dans cette population, déterminez les limites inférieures et supérieures permettant de sélectionner, autour de la moyenne, 68 % - 95 % - 99 % des individus de la population ?
4. Quelle proportion des individus possède une envergure :
   • inférieure à 382,86 mm ?
   • inférieure à 378,795 mm ?
   • supérieure à 421,35 mm ?
5. Une chauve-souris prélevée dans cette population possède une envergure de 405 mm. Appartient-elle à l’intervalle autour de la moyenne isolant 95 % des individus de la population ? En est-il de même avec un individu de 346 mm ?
6. Que vaut approximativement (donnez une fourchette de probabilités) la probabilité de trouver un individu dont la taille serait inférieure à 405 mm ? Refaire l’exercice pour un individu de moins de 346 mm ?

Exercice 2

La pression sanguine chez le rat suit un modèle de Gauss-Laplace. Elle est de 120 mm de Mercure pour une variance de 100 mm².

1. De quel type de variable aléatoire parle-t-on ? Définissez-la en employant la symbolique vue au cours.
2. Quelles sont les limites de pression sanguine telles que la pression sanguine la plus petite de cette zone est inférieure ou égale à 95 % et la plus grande inférieure ou égale à 99 % ? Faites apparaître vos réponses dans un tableau tel que :

   Si s vaut : … mm		Limite inférieure	Limite supérieure
   P(X≤ xi)=…	Zi vaut …

3. Déterminez les limites de l’intervalle autour de moyenne permettant d’isoler 68 % ; 95 % et 99 % pour la population de chauves-souris adultes mâles sachant que la pression sanguine moyenne est aussi de 120 mais la variance est quatre fois moindre par rapport à la variabilité de la population prise dans sa totalité. Comme au point précédent, réalisez un tableau pour résumer vos résultats. Définissez symboliquement cette sous-population.

4. Lorsque la variance diminue, comme c’est le cas dans cet exercice, comment évolue la fonction f(x), notamment au niveau de la densité de probabilité lorsque X = µ ? Comparez ces valeurs pour la population totale de chauves-souris et la sous-population des mâles.