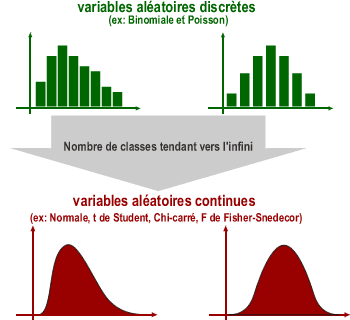
Les variables aléatoires discrètes et continues

Il existe deux grands types de variables aléatoires: les variables discontinues (ou discrètes) et les variables continues.

Les variables aléatoires discrètes

Nous envisageons des variables aléatoires discrètes (X) qui ne peuvent prendre que des valeurs entières positives ou nulles. La distribution des ces variables se représente par un diagramme en barres avec, en abscisse, les valeurs individuelles x_i et, en ordonnée, la probabilité. Pour un échantillon de données, la probabilité sera estimée par la fréquence relative.

Exemple: les distributions binomiales et de Poisson.

Les variables aléatoires continues

Nous envisageons des variables aléatoires continues (X) qui peuvent prendre n'importe quelles valeurs entre deux bornes, éventuellement entre + ou - l'infini. Comme il existe une infinité de valeurs entre deux valeurs x et x+Δ_x (Δ_x tendant vers 0), la probabilité que la variable prenne la valeur exacte x_i est nulle: P(X=x_i)=0.

La distribution des ces variables continues se représente par une fonction continue ou densité de probabilité en fonction des valeurs de la variable. Dans le cas d'un échantillon, la distribution sera représentée par un histogramme avec, en abscisse, les classes de valeurs et, en ordonnée, la fréquence relative ou la densité de fréquences relative (féquence relative divisée par l'intervalle de classe).

Pour établir un histogramme, les valeurs x_i doivent être regroupées en classes.

La variable X est représentée en abscisse. En ordonnée, on représente la densité de fréquences relatives ou, pour n tendant vers l'infini, la densité de probabilités.

Exemple: Parmi ces distributions figurent les distributions normales, normales réduites, t de Student, chi-carré et F de Fisher-Snedecor.