Notions générales de statistique
Probabilités
Convention: les évènements
Les probabilités vues dans ce cours font intervenir des évènements.
Par exemple imaginons d'étudier des drosophiles, et, plus particulièrement, la couleur des yeux et la taille des ailes.
Afin de simplifier les équations à venir, l'évènement "avoir des ailes normales" est noté A et l'évènement "avoir des yeux rouges" est noté B.
L'évènement A ("avoir des ailes normales") est opposé à A* c'est-à-dire "avoir des ailes anormales". De même, l'évènement contraire de B ("avoir des yeux rouges") est noté B* et représente le fait d'avoir "des yeux d'une autre couleur que rouge".
En pratique, si la probabilité d'avoir des ailes normales dans la population de drosophiles est de 30%, cela implique qu'il y a 70% des drosophiles qui ont des ailes différentes de la normale (courtes, courbées, doubles, etc.). On écrira alors:
| TeX Embedding failed! |
| TeX Embedding failed! |
Diagramme de Venn
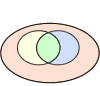
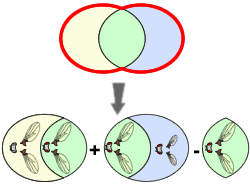
Schématiquement, des événements peuvent être représentés sous la forme d'ensembles "emboîtés" les uns dans les autres pour former un diagramme de Venn.

Soit l'étude porte sur les drosophiles. Dans la population de drosophiles (en rose), il existe des drosophiles avec des ailes normalement constituées et des drosophiles avec des yeux rouges.
Dans le calcul des probabilités, les formules employées font apparaître les lettres: A et B. Nous utiliserons la convention suivante:
Dans une problématique donnée, le premier événement cité sera nommé A et le second B. Dans l'exemple, l'événement A est l'événement "avoir des ailes normales" et B "avoir des yeux rouges".


Evènements contraires
Par convention, le contraire d'un événement est désigné par la même lettre que l'événement avec une "*" à sa suite.
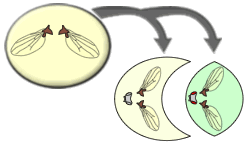
Ainsi, le contraire de l'événement A ("avoir des ailes normales") est l'événement A* ("avoir des ailes non normales"). Sur le diagramme de Venn, cet événement se représente comme suit:
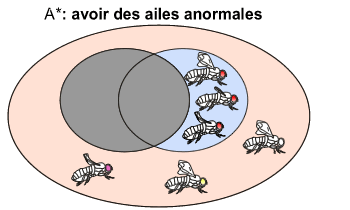
NB: l'événement A est représenté en grisé. Tout le reste (en couleur et montrant des drosophiles de morphologies variées) représente l'événement A*.
De même, le contraire de l'événement B ("avoir des yeux rouges") est l'événement B* ("avoir des yeux d'une autre couleur que rouge") et se représente comme suit:

Intersection
Lorsque deux événements se retrouvent simultanément sur un même individu, on parle d'intersection de ces deux événements. Ainsi, une drosophile qui possède des ailes normales (A) et des yeux rouges (B) est symbolisée de la manière suivante: TeX Embedding failed!
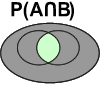
Dans le diagramme de Venn, cette probabilité se représente comme suit:
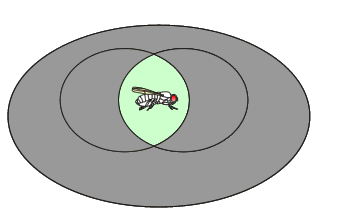
![]() Les zones grisées ne font pas partie de cette probabilité!
Les zones grisées ne font pas partie de cette probabilité!
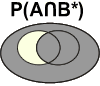
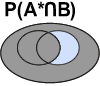
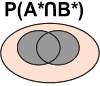
Voici les différentes intersections possibles:
 |
 |
 |
 |
| TeX Embedding failed! | TeX Embedding failed! |
Union
Le fait que deux événements peuvent se réaliser simultanément sur un même individu (intersection) ou seulement un seul (ou aucun) sur un individu s'appelle l'union de deux évènements. Ainsi, une drosophile qui possède des ailes normales (A) ou des yeux rouges (B) est symbolisée de la manière suivante: TeX Embedding failed!
Dans le diagramme de Venn, cette probabilité se représente comme suit:
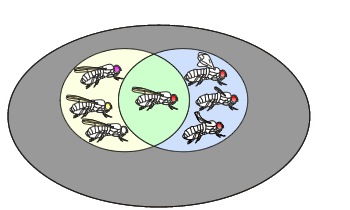
![]() Les zones grisées ne font pas partie de cette probabilité !
Les zones grisées ne font pas partie de cette probabilité !
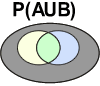
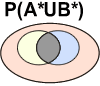
Voici les différentes unions possibles:
 |
 |
||||
 |
 |
||||
|
|
Astuces concernant les unions et les intersections
Le contraire d'une intersection entre deux événements est l'union des 2 événements contraires:
| La probabilité d'intersection | Son contraire |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
| TeX Embedding failed! | TeX Embedding failed! |
| TeX Embedding failed! | TeX Embedding failed! |
![]() Les zones grisées ne font pas partie des probabilités énoncées ci-dessus !
Les zones grisées ne font pas partie des probabilités énoncées ci-dessus !
(In)compatibilités
Soit l'événement A (avoir des ailes normales) et l'événement B (avoir des yeux rouges). S'il est possible de trouver des drosophiles avec des ailes normales (TeX Embedding failed!) ainsi que des drosophiles avec des yeux rouges (TeX Embedding failed!), il est aussi possible de trouver des drosophiles possédant à la fois des ailes normales et des yeux rouges.
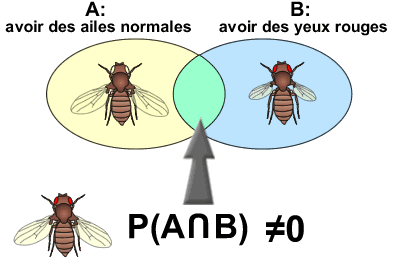
Dans ce cas, la probabilité d'avoir des ailes normales et des yeux rouges ( TeX Embedding failed! ) est non nulle. On dira que les deux événements sont compatibles.
Soit l'événement A (avoir des yeux rouges) et l'événement A* (avoir, par exemple, des yeux jaunes). S'il est possible de trouver des drosophiles avec des yeux rouges ( TeX Embedding failed! ) ainsi que des drosophiles avec des yeux jaunes (TeX Embedding failed!), il est par contre impossible de trouver des drosophiles possédant à la fois un oeil rouge et un oeil jaune.
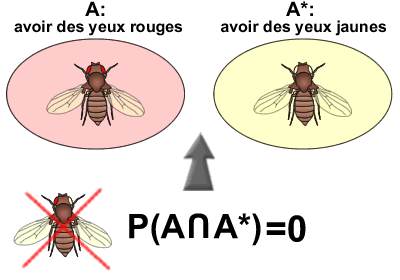
Dans ce cas, la probabilité d'avoir des yeux rouges et des yeux jaunes ( TeX Embedding failed! ) est nulle. On dira que les deux événements sont incompatibles. Remarquons qu'un événement est toujours incompatible avec son événement contraire.
(In)dépendance
Indépendance
Soit une pièce de monnaie équilibrée. Lorsqu'on la lance en l'air, elle ne peut retomber que sur le côté "pile" ou sur le côté "face": p(pile) = 0,5. Considérons les résultats de plusieurs lancers et les événements:
A = avoir pile au premier lancer
B= avoir pile à un lancer ultérieur


|
10 PREMIERS LANCERS: Sur 10 lancers, on peut obtenir, par chance, 10 fois la face PILE. |
p(pile)10 = 0,000976... | |
|
11ème LANCER: Au 11ème lancer, la chance de faire un "pile" ou de faire un "face" est toujours la même, c'est-à-dire 1 chance sur 2 (0,5). La probabilité de faire un FACE au 11ème lancer ne dépend pas du fait qu'on ait fait un PILE aux 10 premiers lancers. On dira que les deux événements sont INDÉPENDANTS. |
p(face/pile) =p(face) = 0,5 |
NOMENCLATURE:
1. p(face/pile) est une probabilité conditionnelle. Elle peut se traduire de la manière suivante:
| p | (face | / | pile) |
| Probabilité de |
faire un face au second lancer
|
Sachant que Dans le contexte de |
on a eu un pile au premier lancer
|
2. D'une manière générale, lorsque l'on dispose de 2 événements A et B indépendants, alors:
TeX Embedding failed! et TeX Embedding failed!
Dépendance
Comparons les hommes et les femmes par rapport à la consommation d'alcool.
Soit P(A) la probabilité d'être une femme et P(B) la probabilité d'avoir un taux d'alcoolémie > 0,5g/l après 3 bières.
Biochimiquement, il a été prouvé que les hommes résistent mieux à l'alcool que les femmes.
Cela implique que:
 |
TeX Embedding failed! | La probabilité d'être saoul sachant qu'on est une femme est différente de la probabilité d'être saoul. |
| TeX Embedding failed! | La probabilité d'être saoul sachant qu'on est un homme est différente de la probabilité d'être saoul. |
NOMENCLATURE:
D'une manière générale, lorsque l'on dispose de 2 événements A et B dépendants, alors:
TeX Embedding failed! et TeX Embedding failed!
Probabilités conditionnelles
Supposons que les événements A (avoir des ailes normales) et B (avoir des yeux rouges) soient compatibles : TeX Embedding failed!.
Lorsque l'on souhaite connaître la proportion de drosophiles aux yeux rouges parmi les drosophiles aux ailes normales, on va donc étudier la probabilité TeX Embedding failed!.
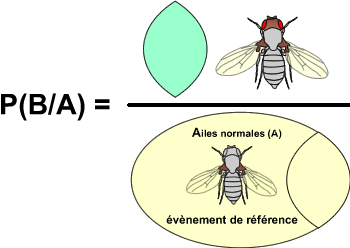
C'est-à-dire, en termes mathématiques:
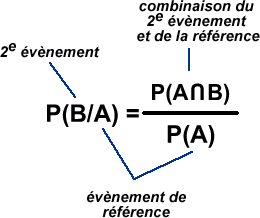
![]() Pour décomposer une probabilité conditionnelle, il suffit de mettre au numérateur l'intersection entre les deux événements apparaissant dans la probabilité conditionnelle et au dénominateur la probabilité de l'événement de référence.
Pour décomposer une probabilité conditionnelle, il suffit de mettre au numérateur l'intersection entre les deux événements apparaissant dans la probabilité conditionnelle et au dénominateur la probabilité de l'événement de référence.
Différents types de probabilités conditionnelles:
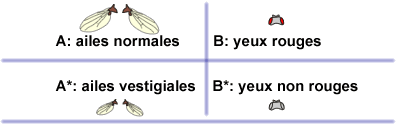
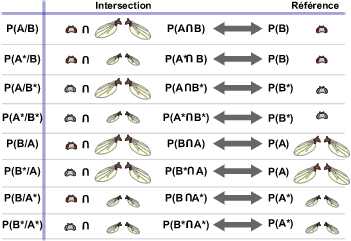
Loi des probabilités totales
Cette loi permet de décomposer la probabilité d'une union en une série d'autres probabilités.
| TeX Embedding failed! |
Ainsi, la probabilité de trouver des drosophiles aux ailes normales (A) ou des drosophiles aux yeux rouges (B) peut se décomposer de la façon suivante:


En d’autres termes, la probabilité de trouver des drosophiles avec des ailes normales OU des yeux rouges s’obtient en additionnant la probabilité d’avoir des ailes normales quelle que soit la couleur des yeux à la probabilité d’avoir des yeux rouges quelles que soient les ailes (normales ou non) des drosophiles. À ce résultat, il faut cependant retirer la probabilité d’observer simultanément les drosophiles ayant à la fois les ailes normales et les yeux rouges (P(A∩B)) car cet événement se retrouve inclus à la fois dans l’ensemble A et dans l’ensemble B. Il est donc comptabilisé deux fois, d’où la nécessité de le retirer une fois pour éviter les doublons.
Décomposition des probabilités d'union suivant la loi des probabilités totales:
| TeX Embedding failed! |
| TeX Embedding failed! |
| TeX Embedding failed! |
| TeX Embedding failed! |
Loi des probabilités composées
Cette loi permet de décomposer une probabilité d'intersection entre deux événements, en un produit de probabilités.
| TeX Embedding failed! |
| TeX Embedding failed! |
Cette loi est basée sur de la notion de probabilité conditionnelle vue précédemment...

C'est-à-dire, en termes mathématiques:

Comme la probabilité d'une intersection se retrouve à la fois dans la zone de l'événement A et de l'événement B, il est possible de comparer cette interaction par rapport à un de ces événements.
Décomposition des probabilités d'intersection suivant la loi des probabilités composées:
| TeX Embedding failed! |
| TeX Embedding failed! |
| TeX Embedding failed! |
| TeX Embedding failed! |
![]() Pour décomposer une probabilité d'intersection, écrivez la probabilité d'un événement seul (la référence), puis, écrivez "multiplié" et enfin, inscrivez la probabilité conditionnelle P(autre événement / événement de référence):
Pour décomposer une probabilité d'intersection, écrivez la probabilité d'un événement seul (la référence), puis, écrivez "multiplié" et enfin, inscrivez la probabilité conditionnelle P(autre événement / événement de référence):
| TeX Embedding failed! |
Décomposition de p(A)
Un évènement complet peut être décomposé en deux intersections:
| TeX Embedding failed! |
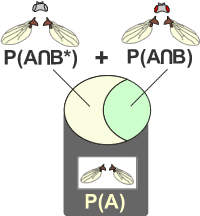
La probabilité d'avoir des ailes normales (A) regroupe les drosophiles aux ailes normales (A) et aux yeux non rouges (B*) ainsi que les drosophiles aux ailes normales (A) et aux yeux rouges (B).
L'obtention de la probabilité de trouver des drosophiles aux ailes normales (A) et aux yeux non rouges (B*) peut être comme suit:
La superposition de l'évènement A et de l'évènement B* permet de mettre en évidence une zone de recouvrement commune aux deux évènements A et B*.

![]() Pour décomposer une probabilité d'un évènement (par exemple A) en une somme d'intersections: dans les deux intersections, vous devez retrouver l'évènement (A) tel quel, l'autre évènement prend une "*" dans une des deux intersections.
Pour décomposer une probabilité d'un évènement (par exemple A) en une somme d'intersections: dans les deux intersections, vous devez retrouver l'évènement (A) tel quel, l'autre évènement prend une "*" dans une des deux intersections.
Décomposition des différents évènements:
| TeX Embedding failed! |
| TeX Embedding failed! |
| TeX Embedding failed! |
| TeX Embedding failed! |
Table de contingence
Une table de contingence est un outil permettant de résoudre rapidement et facilement des problèmes de probabilités.
Une table de contingence est un tableau qui se présente ainsi :
| A | A* | ||
|---|---|---|---|
| B | TeX Embedding failed! | TeX Embedding failed! | TeX Embedding failed! |
| B* | TeX Embedding failed! | TeX Embedding failed! | TeX Embedding failed! |
| TeX Embedding failed! | TeX Embedding failed! | 1 |
Une table de contingence comprend donc toutes les probabilités d'évènements, ainsi que celles des intersections possibles entre évènements.
Le principe de calcul est que chaque cellule de fin de ligne ou de fin de colonne est la somme des deux cellules qui précèdent.
Ainsi, pour les lignes :
| TeX Embedding failed! |
| TeX Embedding failed! |
| TeX Embedding failed! |
Et pour les colonnes :
| TeX Embedding failed! |
| TeX Embedding failed! |
| TeX Embedding failed! |
Pour bien comprendre les relations au sein d'une table de contingence, prenons les illustrations des diagrammes de Venn :
| A | A* | ||
|---|---|---|---|
| B | TeX Embedding failed!
|
TeX Embedding failed!
|
TeX Embedding failed!
|
| B* | TeX Embedding failed!
|
TeX Embedding failed!
|
TeX Embedding failed!
|
| TeX Embedding failed!
|
TeX Embedding failed!
|
1
|
Exercices
1. Soit une population comptant autant d'hommes que de femmes. On sait qu’il y a une chance sur deux d'être saoul après 5 bières. Un homme a 30% de chance d'être saoul après avoir bu 5 bières. Répondez aux questions suivantes :
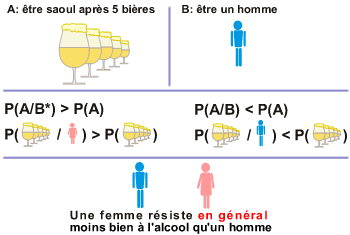
- La probabilité d'être saoul après 5 bières dépend-elle du sexe? (Justifiez numériquement votre réponse)
- Quelle est la probabilité de ne pas être saoul après 5 bières ou d'être un homme?
- Quelle est la probabilité d'être une femme et que celle-ci ne soit pas saoule après 5 bières?
- Quelle est la probabilité de ne pas être saoule après 5 bières alors qu'on est une femme?
- Quelle est la probabilité pour un homme de ne pas être saoul après 5 bières?
2. Une certaine réaction permet de détecter la présence d’une substance dans des prélèvements d’eau. Lorsque la substance est présente, la réaction est positive dans 90% des cas. Lorsque la substance est absente, la réaction est toujours négative. Quelle est la probabilité que la substance soit présente, lorsque la réaction est positive ? La probabilité d’avoir la substance dans un prélèvement étant de 25%.
3. La probabilité d’être de sexe masculin est de 0,5. La probabilité qu’un individu de sexe masculin soit de groupe sanguin A est de 0,40. La probabilité d’être d’un autre groupe sanguin que A est de 0,60.
- Quelle est la probabilité d’être une femme de groupe sanguin A ?
- Quelle est la probabilité d’être du groupe sanguin A ?
- Quelle est la probabilité qu’un individu de groupe sanguin A soit de sexe masculin ?
4. Les eaux peuvent être polluées par la présence d’une bactérie A ou par celle d’une bactérie B. On a constaté la présence de A dans 20% des prélèvements et la présence de B dans 10% des prélèvements, 75% étant exempts de bactéries. Quelle est la probabilité qu’un prélèvement contaminé par B soit également contaminé par A ?
5. Parmi les enfants traités par un vaccin anti-grippe, 20% ont fait une poussée grippale durant les 2 mois qui ont suivi l’administration du vaccin. Durant la même période, parmi les enfants non traités, 46% des enfants ont fait une poussée grippale. Quelle est la probabilité d’être grippé sachant qu’un enfant sur quatre reçoit le vaccin ?
6. Considérons une population de drosophiles. La probabilité d’avoir une drosophile de grande taille est de 0,29. La probabilité d’avoir une drosophile avec des yeux blancs est de 0,13. Il y a indépendance entre la taille et la couleur des yeux.
- Quelle est la probabilité qu’une drosophile ait des yeux rouges sachant qu’elle est de petite taille ?
- Si on prend une drosophile au hasard, quelle est la probabilité qu’elle soit de petite taille et avec des yeux blancs ?
- Quelle est la probabilité qu’une drosophile aux yeux rouges soit de grande taille ?
- Si on prend une drosophile au hasard, quelle est la probabilité qu’elle ait des yeux rouges ou des yeux blancs ?
7. Lorsqu’une substance est présente dans l’eau, une certaine réaction permet de la détecter. On dira que la réaction est positive. La probabilité d’avoir un prélèvement sans la substance et positif est de 0,003. La probabilité d’avoir un prélèvement sans la substance et négatif est de 0,297. La probabilité d’avoir un prélèvement positif est de 0,528.
- Si on prend un prélèvement au hasard, quelle est la probabilité qu’il soit contaminé par la substance et négatif ?
- On prend un prélèvement au hasard, il est contaminé par la substance, quelle est la probabilité qu’il soit négatif ?
- Si on prend un prélèvement au hasard, quelle est la probabilité qu’il ne contienne pas la substance et que la réaction soit négative ?
- Si on prend un prélèvement au hasard, quelle est la probabilité qu’il soit contaminé par la substance et positif, ou qu’il soit positif ?
8. Un test pour détecter le cancer a été mis au point. La probabilité d’avoir un individu en bonne santé et positif au test est de 0,05. La probabilité d’avoir un individu atteint du cancer et positif au test est de 0,15. La probabilité d’avoir un individu en bonne santé est de 0,5.
- Si on prend un individu au hasard, quelle est la probabilité qu’il soit négatif au test ?
- Si on prend un individu au hasard, quelle est la probabilité qu’il soit en bonne santé et positif au test, ou qu’il soit positif au test ?
- Un individu est négatif au test, quelle est la probabilité qu’il soit en bonne santé ?
- Si on prend un individu au hasard, quelle est la probabilité qu’il soit atteint du cancer et négatif au test ?
- Quelle est la probabilité qu’un individu soit atteint du cancer sachant qu’il est négatif au test ?
9. Des cultures de tissus peuvent être infectées par des bactéries ou par des champignons. La probabilité d’avoir une culture infectée par des champignons est de 0,4152. La probabilité d’avoir une culture sans bactéries est de 0,93. La probabilité d’avoir une culture infectée par des bactéries et par des champignons est de 0,0525.
- Si on prend une culture au hasard, quelle est la probabilité qu’elle soit infectée par des bactéries?
- Y a-t-il indépendance entre infection par bactéries et infection par champignons ?
- Si on prend une culture au hasard, quelle est la probabilité qu’elle soit sans bactéries et sans champignons ?
- Si on prend une culture au hasard, quelle est la probabilité qu’elle soit infectée par des bactéries et sans champignons ?
Formulaire
 |
LOI DES PROBABILITÉS TOTALES: TeX Embedding failed! |
 |
LOI DES PROBABILITÉS COMPOSÉES: Si A et B sont dépendants: |
|
Si A et B sont indépendants: |
|
 |
FORMULE HYBRIDE: TeX Embedding failed! |
Tests diagnostiques qualitatifs
Principe
Un test diagnostique est, en médecine, un test qui permet de poser un diagnostic, c'est à dire distinguer, pour une affection donnée, les individus malades des individus sains.
La validité d'un test diagnostique dépend de plusieurs paramètres comme la sensibilité, la spécificité, les valeurs prédictives, les rapports de vraisemblance, ...
L'analyse de la validité d'un test diagnostique doit tenir compte d'un certain nombre de biais et de problèmes (test de référence imparfait, personnes non-vérifiées, ...).
La comparaison de deux analyses de résultats par la même méthode diagnostique peut également constituer une information intéressante. Cela est rendu possible par le calcul de la concordance entre les deux résultats (index Kappa).
Table de contingence
Les résultats d'un test diagnostique peuvent être représentés sous forme d'une table de contingence qui permet de croiser le résultat du test (positif ou négatif) avec le statut du sujet (malade ou non-malade).
Si l'événement A est "être malade" et l'événement B est "être positif au test", la table de contingence reprenant leurs fréquences (et non leurs probabilités) se construit comme suit:
| A | A* | ||
|---|---|---|---|
| B | A ∩ B | A* ∩ B | B |
| B* | A ∩ B* | A* ∩ B* | B* |
| A | A* |
Quatre combinaisons sont possibles:
a) un vrai positif (VP) est une personne qui est malade et qui présente un test positif.
b) un faux positif (FP) est une personne qui n'est pas malade et qui présente un test positif.
c) un faux négatif (FN) est une personne qui est malade et qui présente un test négatif.
d) un vrai négatif (VN) est une personne qui n'est pas malade et qui présente un test négatif.
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | a | b | a + b |
| Négatif | c | d | c + d |
| a + c | b + d | N |
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | VP | FP | VP + FP |
| Négatif | FN | VN | FN + VN |
| VP + FN | FP + VN | N |
On note N l'ensemble de tous les résultats obtenus.
Sensibilité et spécificité
Sensibilité
La sensibilité (Se) est la probabilité qu'un test réalisé sur une personne malade se révèle positif; autrement dit, que le test soit positif sachant que la personne est malade.
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | a | b | a + b |
| Négatif | c | d | c + d |
| a + c | b + d | N |
La sensibilité correspond donc au nombre de personnes malades et positives au test (vrais positifs) parmi l'ensemble des personnes malades.
| TeX Embedding failed! |
Spécificité
La spécificité (Sp) est la probabilité qu'un test réalisé sur une personne saine se révèle négatif; autrement dit, que le test soit négatif sachant que la personne n'est pas malade.
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | a | b | a + b |
| Négatif | c | d | c + d |
| a + c | b + d | N |
La spécificité correspond donc au nombre de personnes non-malades et négatives au test (vrais négatifs) parmi l'ensemble des personnes non-malades.
| TeX Embedding failed! |
Exemple
Afin d'étudier la validité d'un nouveau test de dépistage d'une maladie, 115 personnes malades et 85 personnes qui ne sont pas malades subissent ce test: 90 personnes sont malades et positives au test tandis que 75 sont saines (non-malades) et négatives au test. Quelles sont la sensibilité et la spécificité de ce test ?
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | 90 | 10 | 100 |
| Négatif | 25 | 75 | 100 |
| 115 | 85 | 200 |
TeX Embedding failed! Une sensibilité de 0,78 signifie que, lorsque le patient est malade, il y a 78% de chance que le test de dépistage de la maladie soit positif.
TeX Embedding failed! Une spécificité de 0,88 signifie que, lorsque le patient n'est pas malade, il y a 88% de chance que le test de dépistage de la maladie soit négatif.
Valeurs prédictives
Lorsque le médecin reçoit le résultat (positif ou négatif) d'un test pratiqué sur un de ses patients, il a besoin de connaitre la probabilité que son patient soit malade ou non.
Valeur prédictive positive
La valeur prédictive positive (VPP) est la probabilité que le patient, dont le test est positif, soit effectivement malade.
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | a | b | a + b |
| Négatif | c | d | c + d |
| a + c | b + d | N |
La valeur prédictive positive correspond donc au nombre de personnes malades et positives au test (vrais positifs) parmi l'ensemble des personnes positives au test.
| TeX Embedding failed! |
Valeur prédictive négative
La valeur prédictive négative (VPN) est la probabilité que le patient, dont le test est négatif, ne soit pas malade.
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | a | b | a + b |
| Négatif | c | d | c + d |
| a + c | b + d | N |
La valeur prédictive négative correspond donc au nombre de personnes non-malades et négatives au test (vrais négatifs) parmi l'ensemble des personnes négatives au test.
| TeX Embedding failed! |
Les valeurs prédictives, positive et négative, dépendent de la prévalence de la maladie.
Exemple
Afin d'étudier la validité d'un nouveau test de dépistage d'une maladie, 115 personnes malades et 85 personnes qui ne sont pas malades subissent ce test: 90 personnes sont malades et positives au test tandis que 75 sont saines (non-malades) et négatives au test. Quelles sont les valeurs prédictives positives et négatives ?
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | 90 | 10 | 100 |
| Négatif | 25 | 75 | 100 |
| 115 | 85 | 200 |
TeX Embedding failed! Une valeur prédictive positive de 0,90 signifie que le patient a 90% de risque d'être malade quand le test de dépistage de la maladie est positif.
TeX Embedding failed! Une valeur prédictive négative de 0,75 signifie que le patient a 75% de chance de ne pas être atteint de la maladie quand le test de dépistage de cette maladie est négatif.
Index de Youden
L'index de Youden (Y) est une mesure de la précision de la méthode de diagnostic. Il dépend de la spécificité et de la sensibilité du test mais pas de la prévalence de la maladie.
| TeX Embedding failed! |
L'index de Youden est compris entre 0 (la méthode de diagnostic n'est pas efficace) et 1 (la méthode est parfaite).
Exemple
Afin d'étudier la validité d'un nouveau test de dépistage d'une maladie, 115 personnes malades et 85 personnes qui ne sont pas malades subissent ce test: 90 personnes sont malades et positives au test tandis que 75 sont saines (non-malades) et négatives au test.
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | 90 | 10 | 100 |
| Négatif | 25 | 75 | 100 |
| 115 | 85 | 200 |
TeX Embedding failed! et TeX Embedding failed!
TeX Embedding failed!
Efficacité diagnostique
L'efficacité diagnostique est la proportion de résultats corrects dans l'ensemble des résultats du test.
Les résultats corrects sont les personnes dont le diagnostic posé suite au test correspond à son statut; il s'agit donc des vrais positifs et des vrais négatifs.
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | a | b | a + b |
| Négatif | c | d | c + d |
| a + c | b + d | N |
| TeX Embedding failed! |
Exemple
Afin d'étudier la validité d'un nouveau test de dépistage d'une maladie, 115 personnes malades et 85 personnes qui ne sont pas malades subissent ce test: 90 personnes sont malades et positives au test tandis que 75 sont saines (non-malades) et négatives au test. Quelle est l'efficacité diagnostique de ce test ?
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | 90 | 10 | 100 |
| Négatif | 25 | 75 | 100 |
| 115 | 85 | 200 |
| TeX Embedding failed! |
Une efficacité diagnostique de 0,825 signifie que 82,5% des résultats obtenus lors du test sont corrects.
Rapports de vraissemblance
Rapport de vraisemblance positif
Le rapport de vraisemblance positif (RV(+)) est le rapport entre la probabilité de présenter un test positif quand la personne est malade et la probabilité de présenter un test positif quand la personne n'est pas malade.
| TeX Embedding failed! |
Rapport de vraisemblance négatif
Le rapport de vraisemblance négatif (RV(-)) est le rapport entre la probabilité de présenter un test négatif quand la personne est malade et la probabilité de présenter un test négatif quand la personne n'est pas malade.
| TeX Embedding failed! |
Exemple
Afin d'étudier la validité d'un nouveau test de dépistage d'une maladie, 115 personnes malades et 85 personnes qui ne sont pas malades subissent ce test: 90 personnes sont malades et positives au test tandis que 75 sont saines (non-malades) et négatives au test. Quels sont les rapports de vraisemblance, positifs et négatifs, de ce test ?
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | 90 | 10 | 100 |
| Négatif | 25 | 75 | 100 |
| 115 | 85 | 200 |
On sait que la sensibilté est de 78% (TeX Embedding failed!) et que la spécificité est de 88% (TeX Embedding failed!).
TeX Embedding failed!
Un rapport de vraisemblance positif de 6,5 signifie qu'il y a six fois et demi plus de chance de présenter un test positif lorsque la personne est malade que lorsque la personne n'est pas malade.
TeX Embedding failed!
Un rapport de vraisemblance négatif de 0,25 signifie qu'il y a quatre fois plus de chance de présenter un test négatif lorsque la personne n'est pas malade que lorsque la personne est malade.
Théorème de Bayes
Le théorème de Bayes permet de déterminer les valeurs prédictives d'un test en connaissant la prévalence de la maladie, la sensibilité et la spécificité du test.
La formule générale du théorème de Bayes peut être retrouvée à partir de la loi des probabilités conditionnelles.
Loi des probabilités conditionnelles: TeX Embedding failed!
Or, il est possible de décomposer les membres de la fraction:
- au numérateur: TeX Embedding failed!
- au dénominateur: TeX Embedding failed!
La formule générale du théorème de Bayes est donc:
| TeX Embedding failed! |
Soient les événements A "être malade " et B "être positif au test" et sachant que p(A) est la prévalence de la maladie (notée p), p(B/A) est la sensibilité et p(B*/A*) est la spécificité, alors le théorème de Bayes, appliqué aux tests diagnostiques, devient:
| TeX Embedding failed! |
| TeX Embedding failed! |
Biais de vérification
Pour qu'une personne soit classée comme malade ou non-malade, il est nécessaire d'utiliser une autre méthode de dépistage de cette maladie ayant déjà fait ses preuves (test de référence).
Toutefois, la vérification par ce test de référence peut ne pas être réalisée chez tous les participants de l'étude. Cela est particulièrement le cas si le test de référence est invasif ou risqué.
Ainsi, une personne ayant subi le nouveau test de dépistage peut être classée dans une des trois catégories suivantes:
- vérifiée et malade (on est certain du résultat du test);
- vérifiée et non-malade (on est certain du résultat du test);
- non-vérifiée (on n'a pas la certitude que le résultat est correct; donc, souvent, on ne les prend pas en compte).
| Vérifié | Non-vérifié | |||
|---|---|---|---|---|
| Malade | Non-malade | Total | ||
| Positif | a | b | t1 | u1 |
| Négatif | c | d | t0 | u0 |
On note:
- t1, l'ensemble des personnes positives et vérifiées;
- t0, l'ensemble des personnes négatives et vérifiées;
- u1, l'ensemble des personnes positives mais non-vérifiées;
- u0, l'ensemble des personnes négatives mais non-vérifiées.
Bien qu'elles ne puissent être classées comme malades ou non-malades, les personnes non-vérifiées doivent être prises en compte lors du calcul de la sensibilité et de la spécificité. Ainsi, les formules utilisées sont modifiées et deviennent:
| TeX Embedding failed! |
| TeX Embedding failed! |
Exemple
Afin d'étudier la validité d'un nouveau test de dépistage d'une maladie, 115 personnes malades et 85 personnes qui ne sont pas malades subissent ce test: 90 personnes sont malades et positives au test tandis que 75 sont saines (non-malades) et négatives au test. Toutefois, 5 personnes positives et 20 personnes négatives au test n'ont pas pu être classées comme malades ou non-malades. En tenant compte de ces personnes non-vérifiées, quelles sont la sensibilité et la spécificité de ce test ?
| Vérifié | Non-vérifié | |||
|---|---|---|---|---|
| Malade | Non-malade | Total | ||
| Positif | 90 | 10 | 100 | 5 |
| Négatif | 25 | 75 | 100 | 20 |
| TeX Embedding failed! |
| TeX Embedding failed! |
La sensibilité du test est de 75,9% tandis que sa spécificité est de 89,6%.
Si on ne tient pas compte des personnes non-vérifiées, la sensibilité et la spécificité apparentes valent respectivement 78% et 88%.
On constate donc que, si on néglige le biais de vérification, la sensibilité réelle du test est sur-estimée tandis que la spécificité réelle est sous-estimée.
Imperfection du test de référence
Le test de référence qui a permis de classer les sujets comme malade ou non-malade n'est pas parfait; il présente une sensibilité et une spécificité propre. Il est indispensable de tenir compte de cette imperfection pour déterminer la sensibilité et la spécificité du test étudié.
Si SeR et SpR sont respectivement la sensibilité et la spécificité du test de référence, les formules utilisées pour le calcul de la sensibilité et de la spécificité réelles du test étudié deviennent:
| TeX Embedding failed! |
| TeX Embedding failed! |
Exemple
Afin d'étudier la validité d'un nouveau test de dépistage d'une maladie, 115 personnes malades et 85 personnes qui ne sont pas malades subissent ce test: 90 personnes sont malades et positives au test tandis que 75 sont saines (non-malades) et négatives au test. Le test qui a permis de classer les participants de cette étude en malade et non-malade a une sensibilité de 0,90 et une spécificité de 0,95. En tenant compte de l'imperfection du test de référence, quelles sont la sensibilité et la spécificité du test étudié ?
| Malade | Non-malade | ||
|---|---|---|---|
| Positif | 90 | 10 | 100 |
| Négatif | 25 | 75 | 100 |
| 115 | 85 | 200 |
| TeX Embedding failed! |
| TeX Embedding failed! |
La sensibilité et la spécificité réelles du test étudié sont respectivement de 81% et 100%.
Résultats incertains
Lorsqu'un test est réalisé, il est possible qu'une partie des résultats ne soient ni positifs, ni négatifs; ils sont alors considérés comme incertains.
La table de contingence construite pour illustrer les résultats est adaptée à cette situation. Deux nouvelles possibilités apparaissent:
- i1, le nombre de résultats incertains chez les personnes malades;
- i0, le nombre de résultats incertains chez les personnes saines.
| Malade | Non-malade | |
|---|---|---|
| Positif | a | b |
| Incertain | i1 | i0 |
| Négatif | c | d |
| a + i1 + c | b + i0 + d |
Plusieurs approches sont possibles pour tenir compte des résultats incertains lors de la détermination de la sensibilité et de la spécificité du test étudié.
Approche 1: situation la plus défavorable.
Dans cette approche, les résultats incertains sont considérés comme:
- négatifs lors du calcul de la sensibilité,
- positifs lors du calcul de la spécificité.
Les formules utilisées pour la détermination de la sensibilité et de la spécificité sont adaptées à cette situation.
La sensibilité devient le rapport entre le nombre de personnes malades et positives et l'ensemble des personnes malades.
| Malade | Non-malade | |
|---|---|---|
| Positif | a | b |
| Incertain | i1 | i0 |
| Négatif | c | d |
| a + i1 + c | b + i0 + d |
| TeX Embedding failed! |
La spécificité devient le rapport entre le nombre de personnes saines (non-malades) et négatives et l'ensemble des personnes saines.
| Malade | Non-malade | |
|---|---|---|
| Positif | a | b |
| Incertain | i1 | i0 |
| Négatif | c | d |
| a + i1 + c | b + i0 + d |
| TeX Embedding failed! |
Approche 2: intervalle entre deux bornes.
Lors de cette approche, la borne inférieure est calculée dans la situation la plus défavorable tandis que la borne supérieure est calculée dans la situation la plus favorable. Ainsi, les résultats incertains sont considérés comme:
- positifs lors du calcul de la sensibilité;
- négatifs lors du calcul de la spécificité.
La borne supérieure de la sensibilité est le rapport entre le nombre de personnes malades et positives, ou considérées comme positives, et l'ensemble des personnes malades.
| Malade | Non-malade | |
|---|---|---|
| Positif | a | b |
| Incertain | i1 | i0 |
| Négatif | c | d |
| a + i1 + c | b + i0 + d |
| TeX Embedding failed! |
La borne supérieure de la spécificité est donc le rapport entre le nombre de personnes saines (non-malades) et négatives, ou considérées comme négatives, et l'ensemble des personnes saines.
| Malade | Non-malade | |
|---|---|---|
| Positif | a | b |
| Incertain | i1 | i0 |
| Négatif | c | d |
| a + i1 + c | b + i0 + d |
| TeX Embedding failed! |
Ainsi, la sensibilité et la spécificité réelles du test sont comprises entre une borne inférieure (cf approche 1) et une borne supérieure.÷
| TeX Embedding failed! |
| TeX Embedding failed! |
Approche 3: rendements.
Cette approche consiste à déterminer la sensibilité et la spécificité sans tenir compte des résultats incertains mais en précisant la proportion de résultats certains (rendements).
La sensibilité est accompagnée de la valeur du rendement positif du test. Ce rendement correspond au rapport entre le nombre de résultats certains chez les malades et l'ensemble des personnes malades.
| Malade | Non-malade | |
|---|---|---|
| Positif | a | b |
| Incertain | i1 | i0 |
| Négatif | c | d |
| a + i1 + c | b + i0 + d |
| TeX Embedding failed! |
La spécificité est accompagnée de la valeur du rendement négatif du test. Ce rendement correspond au rapport entre le nombre de résultats certains chez les personnes saines (non-malades) et l'ensemble des personnes saines.
| Malade | Non-malade | |
|---|---|---|
| Positif | a | b |
| Incertain | i1 | i0 |
| Négatif | c | d |
| a + i1 + c | b + i0 + d |
| TeX Embedding failed! |
Index Kappa
La comparaison des résultats d'une même méthode diagnostique interprétés par deux personnes différentes, ou par une même personne mais à des moments différents, est possible grâce à la détermination de la concordance entre les résultats. L'index Kappa permet de quantifier le niveau de cette concordance.
Lors de la première interprétation (test A), les résultats sont soit positifs, soit négatifs. Lors de la seconde interprétation (test B), par une autre personne ou par la même personne mais à un moment différent, les résultats sont également positifs ou négatifs. Ainsi, quatre combinaisons de résultats apparaissent:
(a) résultat positif au test A et positif au test B;
(b) résultat positif au test A et négatif au test B;
(c) résultat négatif au test A et positif au test B;
(d) résultat négatif au test A et négatif au test B.
Ces combinaisons peuvent être représentées sous forme d'un tableau croisant le résultat obtenu au test A avec celui obtenu au test B.
| Test B | ||||
|---|---|---|---|---|
| Positif | Négatif | |||
| Test A | Positif | a | b | n1 |
| Négatif | c | d | n2 | |
| n3 | n4 | N | ||
On note:
- n1, l'ensemble des résultats positifs lors de la première interprétation (test A);
- n2, l'ensemble des résultats négatifs lors de la première interprétation (test A);
- n3, l'ensemble des résultats positifs lors de la seconde interprétation (test B);
- n4, l'ensemble des résultats négatifs lors de la seconde interprétation (test B);
- N, l'ensemble de tous les résultats.
Les résultats concordent lorsque les deux interprétations amènent à la même conclusion; c'est le cas dans les situations a (test A et test B positifs) et d (test A et test B négatifs).
La comparaison de la fréquence de ces résultats concordants par rapport à l'ensemble des résultats permet d'obtenir la proportion de réponses concordantes observée (Po).
| Test B | ||||
|---|---|---|---|---|
| Positif | Négatif | |||
| Test A | Positif | a | b | n1 |
| Négatif | c | d | n2 | |
| n3 | n4 | N | ||
| TeX Embedding failed! |
Toutefois, une partie de la concordance observée est en fait due au hasard; c'est la concordance aléatoire ou la proportion de résultats concordant par chance (Pc). Cette proportion correspond au rapport entre la somme des produits marginaux des résultats concordants et le carré du nombre total de résultats.
| Test B | ||||
|---|---|---|---|---|
| Positif | Négatif | |||
| Test A | Positif | a | b | n1 |
| Négatif | c | d | n2 | |
| n3 | n4 | N | ||
| TeX Embedding failed! |
L'index Kappa (κ), qui quantifie le niveau de concordance réel entre des résultats, est déterminé en tenant compte des concordances observée et aléatoire.
| TeX Embedding failed! |
Plus la valeur de l'index Kappa se rapproche de 1, plus la concordance des résultats est importante. Celle-ci est qualifiée par différents adjectifs en fonction de la valeur de l'index Kappa.
| Accord | Index Kappa |
|---|---|
| Excellent | ≥ 0,80 |
| Bon | 0,60 ≤ κ < 0,80 |
| Moyen | 0,40 ≤ κ < 0,60 |
| Médiocre | 0,20 ≤ κ < 0,40 |
| Mauvais | 0 ≤ κ < 0,20 |
| Exécrable | < 0 |
L'index Kappa est sensible à la prévalence de la maladie.
Exercices
Exercice 1
Afin de diagnostiquer la présence d'une appendicite chez des patients présentant des douleurs abdominales aigues, on réalise une échographie de la région abdominale. Parmi les 255 patients chez lesquels l'échographie était positive, 235 présentaient effectivement une appendicite. Toutefois, 75 des 585 patients dont l'échographie était négative, présentaient également une appendicite.
- Représentez les données sous forme d'une table de contingence.
- Quelle est la spécificité du diagnostique de l'appendicite par échographie abdominale ? Que signifie la valeur obtenue ?
- Quelle est la sensibilité du diagnostique de l'appendicite par échographie abdominale ? Que signifie la valeur obtenue ?
- Quelle est la valeur prédictive positive du diagnostique de l'appendicite par échographie abdominale ? Que signifie la valeur obtenue ?
- Quelle est la valeur prédictive négative du diagnostique de l'appendicite par échographie abdominale ? Que signifie la valeur obtenue ?
Exercice 2
Une firme désire commercialiser un nouveau test de dépistage d'infection urinaire pour les femmes enceintes (bandelettes urinaires). Afin de vérifier son efficacité, ce nouveau produit est testé sur des échantillons d'urine contenant un taux de leucocytes inférieur à la normale (pas d'infection) et supérieur à la normale (infection). Les résultats de ce test se présentent comme décrits dans le tableau suivant.
| Infection | Pas d'infection | |
|---|---|---|
| Test positif | 27 | 3 |
| Test négatif | 5 | 75 |
Toutefois, en plus des résultats positifs et négatifs, 4 tests ont été considérés comme douteux; 2 chez les femmes présentant une infection et 2 chez les femmes ne présentant pas d'infection urinaire.
Représentez l'ensemble des résultats sous forme d'une table de contingence et déterminez la sensibilité et la spécificité du test en tenant compte des résultats incertains.
Exercice 3
Afin de déceler la présence de calculs rénaux chez des patients se plaignant de douleurs caractéristiques intenses, des radiographies des voies urinaires sont réalisées et interprétées par deux médecins. Sur les 150 clichés analysés, 80 sont jugés positifs par les deux médecins tandis que 15 sont considérés comme positifs par le premier médecin mais négatifs par le second médecin. Ce dernier juge comme positives 90 radiographies.
Déterminez la concordance entre les résultats des deux médecins.
Distributions
Les variables aléatoires discrètes et continues
Il existe deux grands types de variables aléatoires: les variables discontinues (ou discrètes) et les variables continues.
Les variables aléatoires discrètes
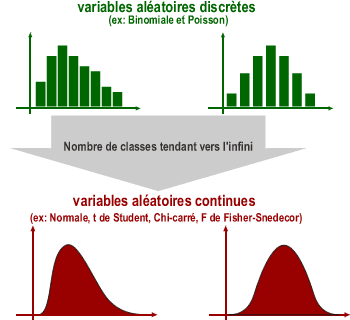
Nous envisageons des variables aléatoires discrètes (X) qui ne peuvent prendre que des valeurs entières positives ou nulles. La distribution des ces variables se représente par un diagramme en barres avec, en abscisse, les valeurs individuelles xi et, en ordonnée, la probabilité. Pour un échantillon de données, la probabilité sera estimée par la fréquence relative.
Exemple: les distributions binomiales et de Poisson.
Les variables aléatoires continues
Nous envisageons des variables aléatoires continues (X) qui peuvent prendre n'importe quelles valeurs entre deux bornes, éventuellement entre + ou - l'infini. Comme il existe une infinité de valeurs entre deux valeurs x et x+Δx (Δx tendant vers 0), la probabilité que la variable prenne la valeur exacte xi est nulle: P(X=xi)=0.
La distribution des ces variables continues se représente par une fonction continue ou densité de probabilité en fonction des valeurs de la variable. Dans le cas d'un échantillon, la distribution sera représentée par un histogramme avec, en abscisse, les classes de valeurs et, en ordonnée, la fréquence relative ou la densité de fréquences relative (féquence relative divisée par l'intervalle de classe).
Pour établir un histogramme, les valeurs xi doivent être regroupées en classes.
La variable X est représentée en abscisse. En ordonnée, on représente la densité de fréquences relatives ou, pour n tendant vers l'infini, la densité de probabilités.
Exemple: Parmi ces distributions figurent les distributions normales, normales réduites, t de Student, chi-carré et F de Fisher-Snedecor.
Approximer une variable aléatoire discrète par une variable aléatoire normale
Les distributions des variables aléatoires discrètes binomiales et de Poisson se représentent par des diagrammes de barres et s’emploient dans les conditions particulières suivantes :
- La variable aléatoire binomiale représente le nombre de succès parmi n épreuves élémentaires. Pour chaque épreuve, on a une probabilité constante de succès π (probabilité d'échec=1-π) (voir aussi le module v.a. binomiale) et les n épreuves sont indépendantes.
- La variable aléatoire de Poisson recense le nombre de réalisations d'un événement par unité de temps, de surface, de volume, etc. (voir aussi le module v.a. de Poisson)
Les distributions des ces 2 variables tendent vers une distribution aléatoire normale dans certaines conditions :
X v.a. Bi (n;π) avec n supérieur à 25 et π proche de 0,5 peut être approximée par une variable aléatoire normale avec moyenne =n.π et variance=n.π(1-π)
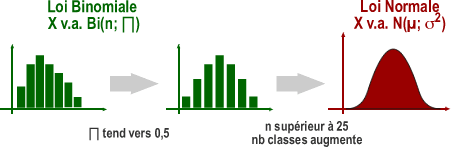
X v.a. Po (µ) avec µ supérieur à 10 peut être approximée par une variable aléatoire normale avec moyenne et variance = µ
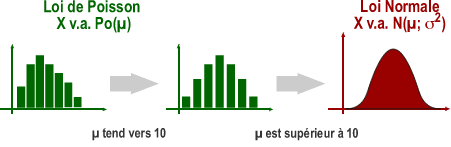
Distributions continues: la variable aléatoire normale (X) et la variable aléatoire normale réduite (Z)
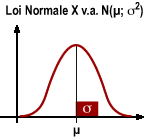
La loi normale caractérise les variables continues dont la fonction de densité de probabilité suit une courbe de Gauss-Laplace : elle est notée X v.a. N (µ ; σ²). La fonction de densité de probabilité dépend de 2 paramètres: la moyenne µ et la variance σ², qui sont propres à chaque variable. Calculer la probabilité que X soit inférieure à une valeur x revient à intégrer la fonction de densité de probabilité jusqu'à la valeur x. Beaucoup de variables biologiques obéissent à un tel modèle.
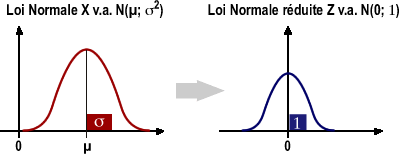
Toute variable aléatoire normale moyenne µ et la variance σ² peut se ramener, par simple transformation algébrique, à une variable aléatoire normale centrée sur 0 et de variance 1 : c’est la variable aléatoire réduite Z [ Z v.a. N (0 ;1)]. La conversion se fait par l’intermédiaire de la formule suivante :
| TeX Embedding failed! |
L'avantage de la distribution normale réduite est qu'elle est unique et qu'il existe une seule table donnant les probabilités pour un grand nombre de valeurs de Z. Calculer la probabilité que P[X<x] revient à calculer la P[Z<z] avec TeX Embedding failed!
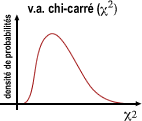
Distributions continues asymétriques (Chi-carré et F de Fisher)
La variable Chi-carré est une somme de variables aléatoires normales réduites au carré (une somme de z2). Sa distribution est asymétrique et dépend d'un seul paramètre k ou nombre de degrés de liberté. Ce nombre de degrés de liberté dépend du nombre de variables aléatoires normales indépendantes intervenant dans la somme.
Exemple : dans certains contextes expérimentaux, l’expérimentateur est amené à comparer des fréquences observées (fobs) à des fréquences prédites par un modèle (fth). Pour chaque catégorie (classe), il est possible de calculer des différences observées réduites au carré (Chi-carré).
Comparons la formule de z et de chi carré: TeX Embedding failed! et TeX Embedding failed! basée sur la propriété que, pour une variable aléatoire de Poisson, la moyenne m est égale à la variance σ2 et qu'ils sont tous deux estimés par fth. La valeur chi carré observée doit donc être comparée à une distribution Chi-carré avec k degrés de liberté (= nombre de classes moins 1).
Exercices
Exercice 1
Une étude est réalisée sur une population de chauve-souris. L’envergure moyenne est, selon des publications très sérieuses, de (375 ± 15) millimètres.
- De quel type de variable aléatoire parle-t-on ? Définissez-la en employant la symbolique vue au cours
- Quel modèle doit-on associer à cette variable aléatoire ? Aidez-vous du formulaire pour écrire l’équation de ce modèle. Que vaut la densité de probabilité au sommet de la fonction de probabilité du modèle f(x) ?
- Dans cette population, déterminez les limites inférieures et supérieures permettant de sélectionner, autour de la moyenne, 68 % - 95 % - 99 % des individus de la population ?
-
Quelle proportion des individus possède une envergure :
- inférieure à 382,86 mm ?
- inférieure à 378,795 mm ?
- supérieure à 421,35 mm ?
- Une chauve-souris prélevée dans cette population possède une envergure de 405 mm. Appartient-elle à l’intervalle autour de la moyenne isolant 95 % des individus de la population ? En est-il de même avec un individu de 346 mm ?
- Que vaut approximativement (donnez une fourchette de probabilités) la probabilité de trouver un individu dont la taille serait inférieure à 405 mm ? Refaire l’exercice pour un individu de moins de 346 mm ?
Exercice 2
La pression sanguine chez le rat suit un modèle de Gauss-Laplace. Elle est de 120 mm de Mercure pour une variance de 100 mm².
- De quel type de variable aléatoire parle-t-on ? Définissez-la en employant la symbolique vue au cours.
-
Quelles sont les limites de pression sanguine telles que la pression sanguine la plus petite de cette zone est inférieure ou égale à 95 % et la plus grande inférieure ou égale à 99 % ? Faites apparaître vos réponses dans un tableau tel que :
Si s vaut : … mm
Limite inférieure
Limite supérieure
P(X≤ xi)=…
Zi vaut …
- Déterminez les limites de l’intervalle autour de moyenne permettant d’isoler 68 % ; 95 % et 99 % pour la population de chauves-souris adultes mâles sachant que la pression sanguine moyenne est aussi de 120 mais la variance est quatre fois moindre par rapport à la variabilité de la population prise dans sa totalité. Comme au point précédent, réalisez un tableau pour résumer vos résultats. Définissez symboliquement cette sous-population.
-
Lorsque la variance diminue, comme c’est le cas dans cet exercice, comment évolue la fonction f(x), notamment au niveau de la densité de probabilité lorsque X = µ ? Comparez ces valeurs pour la population totale de chauves-souris et la sous-population des mâles.