Statistiques descriptives
Statistiques descriptives à une dimension
Population et échantillon
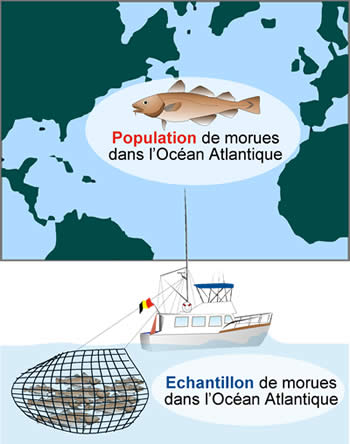
Dans une population de morues atlantiques, il est possible de prélever un échantillon d'individus. C'est cet échantillon qui sera décrit et qui servira de point de départ à une estimation (inférence) ultérieure sur la population.
Les raisons de l'échantillonnage
Parmi les raisons justifiant un échantillonnage plutôt que de travailler sur la globalité de la population:
1: Les ressources sont illimitées...
Il est impossible de pêcher TOUTES les morues de l'Atlantique pour en estimer le poids moyen...
2: Les données disponibles sont limitées...
La reproduction des grands pandas ne peut être étudiée qu'en captivité c'est-à-dire sur un nombre restreint d'individus.

3: L'expérimentation est destructive...
Impossible de sacrifier la population belge de chauves-souris Grand Rhinolophe [200 individus] pour estimer la longueur moyenne de leur intestin grêle.

4: Manque de temps et de moyens
Même dans le cas où la population est limitée, on n'a pas le temps ni les moyens d'effectuer toutes les mesures: par exemple, demander l'avis des consommateurs à propos d'un nouveau produit prendrait trop de temps et nécessiterait des moyens financiers trop importants.
Décrire un ensemble de données
 Supposons que l'on prélève dans les filets de ce chalutier 15 morues atlantiques. Celles-ci constituent l'échantillon.
Supposons que l'on prélève dans les filets de ce chalutier 15 morues atlantiques. Celles-ci constituent l'échantillon.
Chaque individu est pesé (= mesure xi de la variable poids "X") et les résultats sont répertoriés ci-dessous.
Description d'un ensemble de données où une seule variable est mesurée = statistique DESCRIPTIVE à 1 dimension
Variable étudiée: poids en kg = 1 DIMENSION (X)
Une donnée = 1 mesure de poids (xi)
| Individu 1 | Poids 1 | |
Individu 6 | Poids 6 | |
Individu 11 | Poids 11 |
| Individu 2 | Poids 2 | Individu 7 | Poids 7 | Individu 12 | Poids 12 | ||
| Individu 3 | Poids 3 | Individu 8 | Poids 8 | Individu 13 | Poids 13 | ||
| Individu 4 | Poids 4 | Individu 9 | Poids 9 | Individu 14 | Poids 14 | ||
| Individu 5 | Poids 5 | Individu 10 | Poids 10 | Individu 15 | Poids 15 |
Statistique descriptive:
La description de l'ensemble des données se poursuit par le classement des données, les mesures de la tendance centrale et de la dispersion.
Classer les données

TRI DES POISSONS EN FONCTION DE LEUR POIDS DANS PLUSIEURS CLASSES

Le nombre de classes dépend du nombre d'individus pêchés:
-
- il ne peut être trop petit sous peine de perdre de l'information: 1 ou 2 classes contenant tous les individus de l'échantillon simplifie à outrance les données;
- il ne peut être trop grand sous peine d'avoir trop de classes vides: pour un échantillon de 15 individus, réaliser 15 classes revient à avoir des classes ne contenant même pas un poisson.
-
- classe 1: de 0 Kg inclus à 2 Kg exclus
- classe 2: de 2 Kg inclus à 4 Kg exclus
- classe 3: de 4 Kg inclus à 6 Kg exclus
- classe 4: de 6 Kg inclus à 8 Kg exclus
- fréquence: nombre d'individus appartenant à une classe. Il est généralement noté ni . La somme des fréquences de toutes les classes est la taille de l'échantillon N.
- fréquence cumulée: somme des fréquences de la classe étudiée et des fréquences des classes qui lui sont inférieures. La fréquence cumulée de la dernière classe vaut N (c'est-à-dire la somme des ni).
- la fréquence relative: rapport entre la fréquence de la classe étudiée et la taille de l'échantillon. Nous étudions dans ce cas l'importance de la classe par rapport à la globalité de l'échantillon (exemple: 20% des individus de l'échantillon présenté dans la figure ci-dessus ont une envergure comprise entre 380 et 400 mm). La somme de toutes les fréquences relatives est égale à 1. Elle est notée TeX Embedding failed! et souvent exprimée en %.
- la fréquence relative cumulée: somme des fréquences relatives de la classe étudiée et des classes qui lui sont inférieures. La fréquence relative cumulée de la dernière classe vaut 1 (ou 100%).
-
la densité de fréquences relatives : souvent employée pour que la surface de chaque rectangle de l'histogramme corresponde à la fréquence relative de la classe:
Surface d'un rectangle = hauteur x base = TeX Embedding failed! ou encore, après simplification des Li, la fréquence relative: TeX Embedding failed!.
Un cas extrême est celui où la taille de l'échantillon tend vers l'infini. A ce moment, le nombre de classes possibles tend aussi vers l'infini. Chaque classe possède un intervalle (une base) infinitésimal. La surface d'un rectangle tend vers 0. On ne parlera plus de distribution de densités de fréquences relatives mais de distribution de densités de probabilités.
L'intervalle de classe (Li) est la distance séparant la limite supérieure de la limite inférieure de chaque classe.
Exemple de tableau de fréquences et histogrammes associés
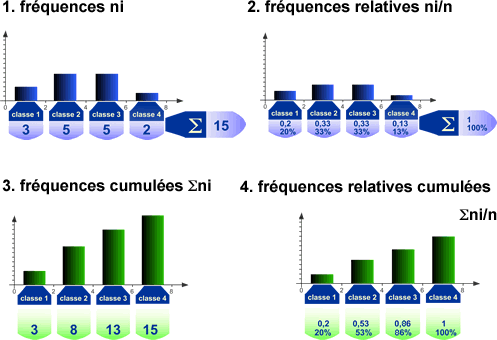
| Classe 1 | Classe 2 | Classe 3 | Classe 4 | Total | |
| Fréquences | 3 | 5 | 5 | 2 | 15 |
| Fréquences relatives | 0,2 | 0,33 | 0,33 | 0,13 | 1 |
| Fréquences cumulées | 3 | 8 | 13 | 15 | x |
| Fréquences relatives cumulées | 0,2 | 0,53 | 0,86 | 1 | x |
Les mesures de tendance centrale
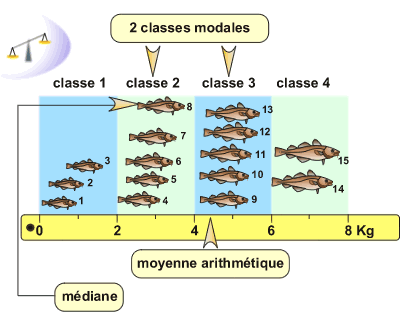
La moyenne arithmétique est la mesure de la tendance centrale la plus facile à calculer. Elle est obtenue par la division de la somme de toutes les valeurs de l'échantillon par la taille de l'échantillon (n). Cette mesure est sensible aux valeurs extrêmes.
Le mode détermine la valeur la plus fréquente dans un échantillon. Si l'échantillon est divisé en classes, la classe modale constitue la classe la plus fréquente. Dans l'exemple ci-dessus, les classes modales sont les classes 2 et 3 et contiennent 5 individus chacune.
La médiane est la valeur telle que 50% des observations de l'échantillon lui sont inférieures ou supérieures. Son calcul nécessite de classer les observations de la plus petite à la plus grande.
- Si le nombre d'observations est pair: la médiane est la moyenne des observations TeX Embedding failed! et TeX Embedding failed!.
- Si le nombre d'observations est impair: la médiane est la valeur TeX Embedding failed!. Dans l'exemple ci-dessus, l'échantillon est composé de 15 individus. Cela implique que la médiane correspond au poids de l'individu n°8. En effet, il existe 7 individus de taille inférieure à la médiane et 7 individus de taille supérieure à cette même médiane.
Les mesures de dispersion
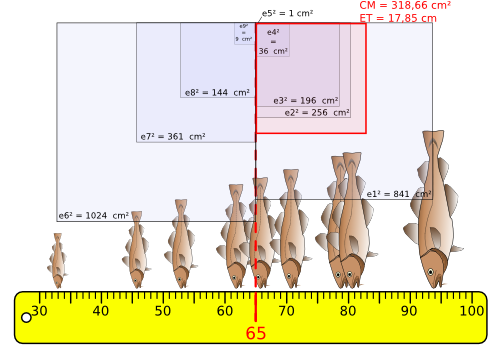
Pour illustrer les mesures de dispersion, prenons pour exemple un échantillon de 9 morues de l'Atlantique (Gadus morhua).

Pour cet échantillon de 9 morues, nous allons étudier la dispersion de la taille de ces poissons en calculant les paramètres suivants :
Pour commencer, mesurons la taille de ces 9 poissons, ainsi que la moyenne de ces tailles, qui vaut ici 65 cm :
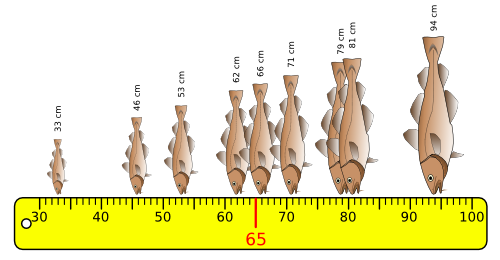
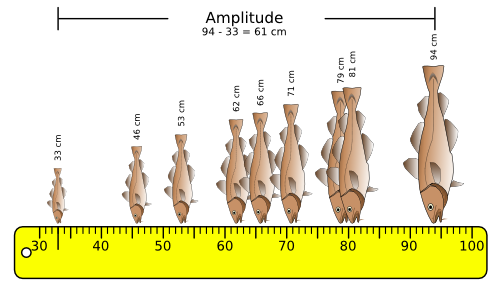
L'amplitude :
Définition : L'amplitude (ou étendue) d'un échantillon est l'écart qui sépare la valeur la plus petite de la valeur la plus grande.
Formule : amplitude = valeur maximale - valeur minimale
Domaine : L'amplitude peut prendre des valeurs qui vont de 0 à l'infini.
La variance :
Définition : La variance est le reflet numérique de la dispersion des valeurs autour de la moyenne.
Elle est obtenue à partir des écarts des valeurs par rapport à la moyenne.
Ecarts à la moyenne :
Pour chaque valeur on calcule l'écart qui le sépare de sa moyenne arithmétique : TeX Embedding failed!
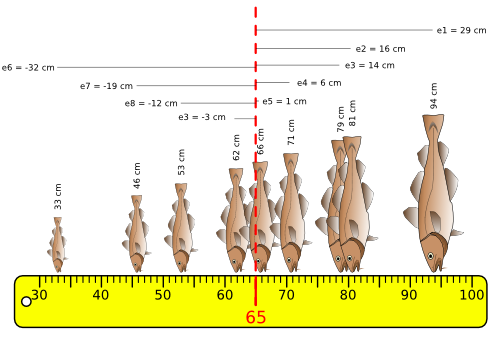
La somme de ces écarts est nulle. Elle ne peut donc être utilisée comme un estimateur mathématique de la dispersion des valeurs.
Carrés des Ecarts à la moyenne :
Pour chacun des écarts précédents, on calcule son carré. Ainsi pour chaque valeur on obtient une valeur positive, et leur somme n'est jamais nulle, sauf si les écarts sont nuls (valeurs égales à la moyenne).
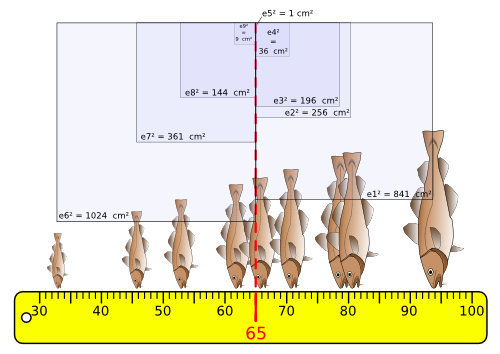
Si on additionne tous ces carrés d'écarts :
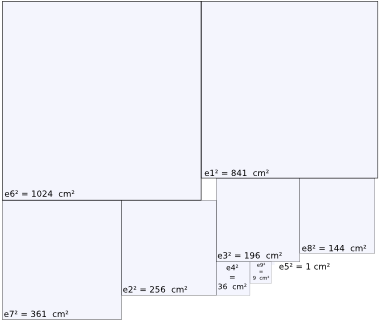
Cela donne :

La somme des carrés des écarts (SCE) sera d'autant plus grande que les valeurs seront éloignées de la moyenne. C'est donc un bon estimateur de la dispersion des valeurs autour de la moyenne.
| TeX Embedding failed! |
Cependant, à dispersion équivalente, la SCE sera toujours d'autant plus grande qu'il y aura un nombre important de valeurs. Pour que le paramètre de dispersion soit indépendant du nombre de valeurs, on calcule le carré moyen ou la variance.
Carré moyen ou variance :
Le carré moyen ou variance représente la surface moyenne des carrés d'écarts. C'est la SCE/n.
Elle caractérise la distribution des valeurs autour de la moyenne.
Elle est exprimée dans le carré des unités des valeurs, ici en cm2.
Formule : Elle se calcule en sommant les carrés des écarts (SCE = Somme de Carrés des Écarts), et en divisant cette somme par le nombre de valeurs.
| TeX Embedding failed! |
Domaine : La variance est comprise entre 0 et l'infini.
A partir des données numériques d'un échantillon, il est aussi possible d'estimer la variance de la population d'où provient cet échantillon. Dans ce cas, la somme des carrés des écarts est divisée par n-1 et non par n. Quand le nombre d'observations est élevé, la division par n-1 ou par n n' a plus beaucoup d'importance.
| TeX Embedding failed! |
L'écart-type :
La variance étant exprimée dans le carré des unités, on lui préfère souvent l'écart-type, ou racine carrée de la variance. L'écart-type a les mêmes unités que les données et que la moyenne.
Définition : L'écart-type représente l'écart quadratique moyen des valeurs par rapport à la moyenne.
Formule : L'écart-type (ET ou S) est la longueur du côté du carré moyen. Selon que l'on veut simplement décrire l'ensemble des données ou estimer l'écart-type de la population d'origine, on utilisera la racine carrée de la variance SCE/n ou SCE/(n-1)
| TeX Embedding failed! |
Domaine : L'écart-type est compris entre 0 et l'infini.
Le coefficient de variation :
Définition : Le coefficient de variation représente le rapport de l'écart-type par la moyenne.
Formule :
| TeX Embedding failed! |
Domaine : Le coefficient de variation est compris entre 0 et l'infini.
Utilisation : Le CV est indépendant des unités de mesure. Il permet de comparer la dispersion de données exprimées dans des unités de mesure différentes (par exemple, poids exprimé en kg ou en gr). Il est également utilisé pour comparer la dispersion des mesures quelle que soit la valeur de la moyenne.
Exercices
But du T.P.
Ce T.P. sert à jeter les bases des statistiques descriptives. Il met en place les notions nécessaires à la compréhension des tests d'hypothèses de la fin du cours. Le but est donc de faire prendre conscience aux étudiants de l'importance capitale de cette matière. Contexte expérimental
À la demande de la Région Wallonne, une étude est menée afin de vérifier que les chauves-souris de l'espèce Grand Rhinolophe ne sont pas affectées par l'implantation d'une industrie polluante (pollution au plomb) à proximité de leur habitat.
Une recherche bibliographique a été réalisée et voici les résultats obtenus :
Systématique:
- Rang taxonomique : Vertébrés - Mammifères - Microchiroptera - Rhinolophidae
- Groupe biologique : Vertébrés / Mammifères / Chauve-souris
- Synonyme(s) : Rhinolophus ferrumequinum (Schreber, 1774) [Sources: Lina (1998)]; Rhinolophus ferrum-equinum
- Nom français : Grand rhinolophe Grand fer-à-cheval
- Nom néerlandais : Grote hoefijzerneus
- Nom anglais : Greater horseshoe bat
Caractéristiques morphologiques:
- Longueur tête et corps: 57-71 mm
- Longueur avant-bras: 54-61 mm
- Longueur oreilles: 20-26 mm
- Envergure: 350-400 mm
- Poids: 17-35 g
Pelage roussâtre sur le dos de l'adulte et plus gris chez le jeune. Face ventrale gris-blanc à blanc-jaunâtre.
Il s'agit du plus grand rhinolophe européen.
Ecologie
Il chasse dans les endroits boisés, le long des falaises, ou dans les jardins. Le vol est lent, papillonnant, avec de brèves glissades, à faible hauteur (de 30 cm à 3 m au-dessus du sol). Il se nourrit de grosses proies comme les papillons nocturnes et les coléoptères.
Cette espèce sédentaire atteint sa limite géographique nord approximativement au sillon Sambre et Meuse. Les déplacements entre les gîtes d'hiver et d'été dépassent rarement les 30 km.
Pour la reproduction, le grand rhinolophe a besoin de gîtes volumineux (plus de 100 m3) qu'il peut atteindre en vol direct et dans lesquels il peut évoluer facilement. Les colonies de reproduction peuvent atteindre plusieurs centaines d'individus qui se tiennent généralement à distance les uns des autres. Cette espèce est très souvent associée au vespertilion à oreilles échancrées.
Pour l'hivernage, il choisit des abris souterrains dont la température ambiante se situe entre 7 et 11°C. Il est extrêmement sensible aux dérangements.
Questions
Thème 1 : Les variabilités, précision et inexactitude
Question 1 :
Dans un échantillon, pourquoi les individus sont-ils, en général, tous différents les uns des autres ?
Question 2 : Donnez un nom aux phénomènes suivants :
Situation 1 : J’ai prélevé une chauve-souris au hasard dans une population donnée et je l’ai déposée à 3 reprises sur la même balance. Je m’attendais à obtenir 3 fois le même poids, mais les valeurs obtenues sont très légèrement différentes.
Situation 2 : J’ai prélevé une chauve-souris au hasard dans une population donnée et je l’ai déposée sur une balance. Je sais que le poids obtenu ne sera jamais le poids réel de l’individu mais une approximation de ce poids.
Thème 2 : Distinguer la population et l’échantillon
Question 3 : Soit un échantillon de n chauves-souris capturées aléatoirement dans une population donnée. Dans la littérature scientifique, voici ce que l’on peut trouver :
Caractéristiques morphologiques
- Longueur tête et corps: 57-71 mm
- Longueur avant-bras: 54-61 mm
- Longueur oreilles: 20-26 mm
- Envergure: 350-400 mm
- Poids: 17-35 g
Question 3.1. : Quelles sont les mesures permettant de caractériser au mieux l’échantillon et leur équivalent au niveau de la population ? Nommez-les en expliquant les nuances ?
Question 3.2. : Dans le contexte expérimental décrit avant, que représentent les valeurs obtenues pour les caractéristiques morphologiques ?
Question 4 : Quelles sont les raisons pour lesquelles un échantillonnage est indispensable ?
Thème 3 : tables de fréquences et histogrammes
Soit un échantillon de 15 chauves-souris de l’espèce " Grand Rhinolophe " capturées aléatoirement dans la population.
Question 5 : Comment représenter schématiquement un échantillon de chauves-souris pour lequel on a mesuré le poids de chaque individu ?
Question 6 : Pour le même échantillon, peut-on générer différents graphiques ? Pourquoi et quelles informations peut-on en tirer ? Ce nombre de graphiques possibles est-il illimité ? Dans l’exemple combien de classes peut-on former ?
Question 7 : On sait que l’envergure des chauves-souris est comprise entre 350 et 400 mm. Analysez les différentes situations qui vous sont proposées ci-dessous et découvrez le type de dénombrement employé :
Situation 1 : J’ai réalisé 5 classes d’intervalles constants pour répartir les 15 chauves-souris capturées et j’ai observé que 87 % des individus constituant cet échantillon avaient une envergure inférieure à 390 mm.
Situation 2 : J’ai réalisé 5 classes d’intervalles constants pour répartir les 15 chauves-souris capturées et j’ai observé que 8 individus de cet échantillon avaient une envergure comprise entre 350 et 370 mm.
Situation 3 : J’ai réalisé 5 classes d’intervalles constants pour répartir les 15 chauves-souris capturées et j’ai observé que 20 % des individus constituant cet échantillon avaient une envergure comprise entre 360 et 370 mm.
Situation 4 : J’ai réalisé 5 classes d’intervalles constants pour répartir les 15 chauves-souris capturées et j’ai observé que 5 individus de cet échantillon avaient une envergure comprise entre 370 et 380 mm.
Situation 5 : J’ai réalisé 5 classes d’intervalles constants pour répartir les 15 chauves-souris capturées, quelle est la proportion de chauves-souris dont l’envergure est inférieure à 400 mm ?
Situation 6 : Dans quelles circonstances utilise-t-on des densités de fréquences relatives et pour quelles raisons les utilise-t-on ?
Thème 4 : Tendance centrale et dispersion
Question 8 : Soit un échantillon de 15 chauves-souris prélevées aléatoirement dans une population donnée. Quelles sont les valeurs permettant de décrire au mieux un échantillon ? Définissez-les.
Question 9 : Hors de ces valeurs permettant de décrire un échantillon et que vous venez de définir :
- Déterminez celle(s) qui (est) sont susceptible(s) de changer pour un échantillon composé des mêmes individus.
- Déterminez celle(s) qui permet(tent) de juger de la précision d’un instrument de mesure.
- Qu’évoquent une variance d’échantillon et un estimateur de la variance de la population ? Dans quel cas peut-on égaler ces deux valeurs ?
Question 10 : Soit un échantillon composé de 15 chauves-souris mâles et adultes de l’espèce X.
- Quel type de solution graphique est vraisemblable : distribution de fréquences uniformes quelle que soit la classe, distribution symétrique de type pyramidale, distribution asymétrique avec traînée à gauche ou à droite ?
- Comment les mesures caractérisant la tendance centrale de l’échantillon vont-elles être influencées ?
- Comment feriez-vous pour que votre échantillon obéisse respectivement à chaque modèle de distribution (asymétrie avec traînée à gauche ou à droite) et quelle répercussion cela va-t-il avoir sur les mesures de tendance centrale ?-->
Question 11 : Où se positionne la médiane d’un échantillon de :
- 15 individus ?
- 16 individus ?
Statistiques descriptives à deux dimensions
Définir les statistiques descriptives à deux dimensions
On parle de statistiques à deux dimensions lorsqu'on étudie conjointement deux variables aléatoires, X et Y. On ne cherche plus à caractériser la distribution de chacune des variables, ce qui est du ressort des statistiques à une dimension, mais bien à caractériser leur distribution conjointe.
On se pose donc la question de savoir si la distribution d'une des variables influence ou non celle de l'autre.
Un exemple classique vous est donné à l'illustration ci-dessous: l'envergure et le poids de chauves-souris sont-ils distribués de manière dépendante ou indépendante l'un de l'autre ?
Une chauve-souris a-t-elle forcément un poids important lorsqu'elle a une grande envergure ?
Une chauve-souris a-t-elle forcément une grande envergure lorsqu'elle a un poids important ?
Diagramme de dispersion
Les statistiques à deux dimensions s'appliquent non plus aux valeurs de X et Y considérées de manière individuelle, mais bien aux couples (X;Y), qui représentent les deux mesures qui ont été réalisées sur un même individu.
Dans notre exemple, pour chaque chauve-souris, un couple (envergure; poids) a été mesuré.
L'ensemble de ces points est reporté sur un graphique à deux dimensions, type "nuage de points" ou diagramme de dispersion.
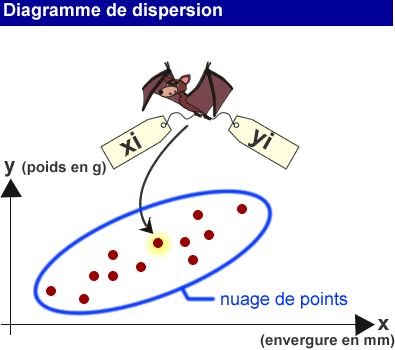
Propriétés du nuage de points et SPE
Le centre de gravité du nuage de points est un point fictif qui a pour coordonnées (moyenne des X; moyenne des Y).
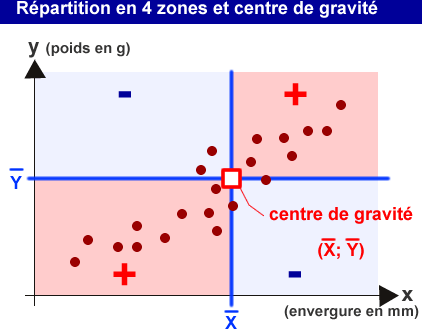
Pour chaque point, on peut quantifier son écart par rapport à ce centre de gravité en réalisant le calcul du produit des écarts:
| TeX Embedding failed! |
Ce produit des écarts est positif pour les points situés dans les quadrants roses du graphique ci-dessus, et négatif s'ils sont situés dans les quadrants bleus. Le nuage de points schématisé dans le graphique ci-dessus a donc des PE majoritairement positifs.
En réalisant la somme de tous ces PE, je peux donc avoir une estimation de l'orientation du nuage de points par rapport à son centre de gravité.
SPE : Somme des Produits des Ecarts
Si la SPE est positive, comme c'est le cas ici, le nuage de points est orienté de manière ascendante dans le sens gauche-droite. Si la SPE du nuage de points est négative, c'est qu'il est orienté de manière descendante.
La SPE amène donc énormément d'informations sur le sens de la relation qui pourrait éventuellement exister entre X et Y.
Note: Dans certaines situations expérimentales il peut être intéressant de comparer des nuages de points provenant d'expériences différentes. Dans ce cas, on doit ramener les deux nuages de points dans une échelle comparable. Pour cela on réalise une réduction des variables X et Y respectives, selon les formules suivantes:
| TeX Embedding failed! |
| TeX Embedding failed! |
Le processus de réduction s'opère en retirant des coordonnées en X et en Y leur moyenne respective. Cela permet de repositionner les deux centres de gravité aux coordonnées identiques de (0;0). Pour éliminer la variabilité propre au contexte expérimental, les différences entre coordonnées (X ou Y) expérimentales et moyennes (de X ou de Y) sont divisées par l'écart-type (de X ou de Y). Par définition, comme les centres de gravité sont aux coordonnées (0;0), la somme des valeurs réduites pour chaque variable est nulle et les écart-types (ou variances) égaux à 1.
Covariance
La valeur de la SPE dépend du nombre de couples de valeurs X et Y. Si on divise la SPE par n, on obtient la covariance ou encore une mesure de la covariation des 2 variables X et Y.
| TeX Embedding failed! |
La covariance est donc le PE moyen du nuage de points. Elle est positive lorsque le nuage de points a une orientation ascendante, et négative lorsque ce nuage a une orientation descendante. Elle a pour unités, les unités de X multipliées par les unités de Y.
Coefficient de corrélation
Le coefficient de corrélation (noté r) est calculé à partir de la covariance:
| TeX Embedding failed! |
Le coefficient de corrélation quantifie l'intensité et le sens de la relation qui existe entre deux variables. C'est un nombre pur sans unités compris entre -1 et +1.
Si les deux variables varient indépendamment l'une de l'autre, sa valeur est de 0. Si les deux variables évoluent parallèlement (Y augmente lorsque X augmente), sa valeur sera positive, avec un maximum de 1 (lorsque l'évolution de Y est directement proportionnelle à celle de x). Si les deux variables évoluent à l'inverse l'une de l'autre, sa valeur sera négative, avec un minimum de -1.
Donc: TeX Embedding failed!
Le coefficient de corrélation entre X et Y dépend de la proximité des points autour de la droite et de l'orientation du nuage de points. Si les points sont tous alignés sur la droite, le coefficient de corrélation est égal à 1 en valeur absolue, pour autant que la pente de la droite soit différente de 0.
Régression et coefficient de détermination
Il est possible de quantifier la relation existant entre les variables X et Y en calculant l'équation de régression de Y en fonction de X
Régression linéaire :
Cette relation peut être linéaire ou non. Dans le cas du modèle linéaire l'équation de la régression est:
Modèle linéaire: TeX Embedding failed!
Les paramètres a (ordonnée à l'origine) et b (pente) peuvent être déterminés selon deux méthodes, la méthode des moindres carrés, ou celle des moindres rectangles, qui seront choisies en fonction du type de relation existant entre X et Y. Ces deux méthodes sont détaillées à la page suivante.
Lors de l'établissement d'une équation de régression, le coefficient de détermination (R²) détermine à quel point l'équation de régression est adaptée pour décrire la distribution des points.
Si le R² est nul, cela signifie que l'équation de la droite de régression détermine 0% de la distribution des points. Cela signifie que le modèle mathématique utilisé n'explique absolument pas la distribution des points.
Si le R² vaut 1, cela signifie que l'équation de la droite de régression est capable de déterminer 100% de la distribution des points. Cela signifie que le modèle mathématique utilisé, ainsi que les paramètres a et b calculés sont ceux qui déterminent la distribution des points.
Cela se traduit de manière graphique selon la relation suivante: plus le coefficient de détermination se rapproche de 0, plus le nuage de points est diffus autour de la droite de régression. Au contraire, plus le R² tend vers 1, plus le nuage de points se rapproche de la droite de régression. Quand les points sont exactement alignés sur la droite de régression, R²=1.
Donc: TeX Embedding failed!
Dans le cas où la méthode des moindres carrés est utilisée pour calculer l'équation, le R² est calculé selon la formule:
| TeX Embedding failed! |
| TeX Embedding failed! |
En fin de module, vous trouverez une animation devant vous permettre, nous l'espérons, de mieux saisir les subtilités relatives au R², mais aussi au r.
NOTE: le R² n'est le carré du coefficient de corrélation que dans le cas particulier de la régression linéaire. Dans les autres régressions (logarithmique, exponentielle, puissance, etc.) ce n'est pas le cas. C'est pour éviter cette confusion facile qu'on note habituellement le r du coefficient de corrélation en minuscule, et celui du coefficient de détermination R² en majuscule.
Droites des moindres carrés
La détermination de la pente (b) et de l'ordonnée à l'origine (a) selon la méthode des moindres carrés:

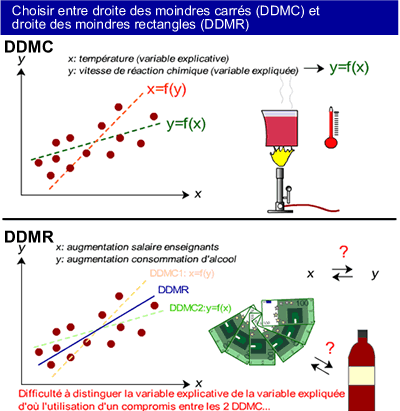
La méthode des moindres carrés est utilisée lorsqu'à priori une relation de cause à effet relie X à Y (lorsque la valeur de Y dépend de X). On distingue alors la variable expliquée Y et la variable explicative X. Dans ce cas, les valeurs de a et de b sont obtenues en minimisant les carrés des distances des points observés TeX Embedding failed! par rapport à la droite.
exemple: C'est parce que la température augmente (X ou variable explicative) que la vitesse de réaction chimique augmente (Y ou variable expliquée), et non l'inverse.
On utilise la droite des moindres rectangles lorsqu'aucune relation de cause à effet n'existe à priori de manière évidente entre X et Y. Dans ce cas, les valeurs de a et de b sont obtenues en minimisant les produits des distances des points observés TeX Embedding failed! et TeX Embedding failed! par rapport à la droite.
Intrapoler ou extrapoler ?
Un des intérêts d'une régression est qu'avec les paramètres a et b on peut estimer des valeurs de Y pour des valeurs de X qu'on n'a pas pu mesurer (car cela coûte cher, ou que c'est difficile à réaliser...).
Cependant, la précision de cette estimation d'une valeur de Y varie fort selon qu'elle est estimée à partir d'un X compris dans l'intervalle des mesures initiales (intrapolation) ou si elle est estimée à partir d'un X situé à l'extérieur de cet intervalle (extrapolation).
Intrapolation :
Intrapolation = Evaluation d'une variable dans les limites de l'échantillon.
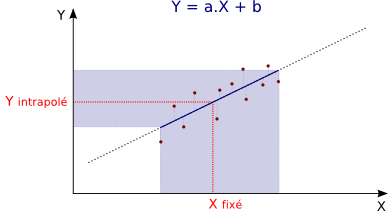
L'intrapolation de la valeur de y correspondant à une valeur mesurée de x est d'autant plus fiable que la valeur x mesurée est proche de la moyenne des X et que l'équation de la droite a été établie avec un R² proche de 1.
Extrapolation :
Extrapolation = Evaluation d'une variable hors des limites de l'échantillon.
Extrapolation pertinente :
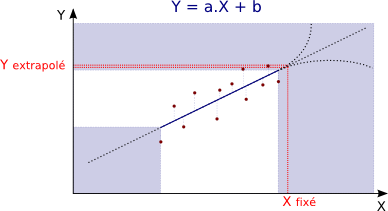
L'extrapolation est d'autant plus pertinente qu'elle est réalisée près des limites de l'échantillon.
Extrapolation aberrante :
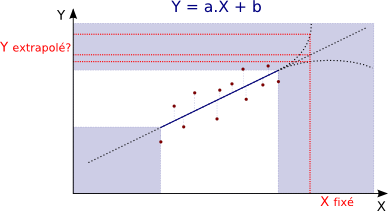
L'extrapolation est d'autant moins fiable qu'on est loin des limites de l'échantillon car le modèle linéaire n'est plus forcément d'application.
Linéarisation de modèles non linéaires
Dans certaines situations expérimentales, la régression linéaire n'est pas appropriée: il faut donc rechercher d'autres modèles pour décrire la relation entre X et Y.
Certains modèles peuvent se ramener à un modèle linéaire par une transformation mathématique des valeurs de X et/ou Y.
Voici quelques modèles de régressions non-linéaires, et leurs transformations respectives pour obtenir une régression linéaire :
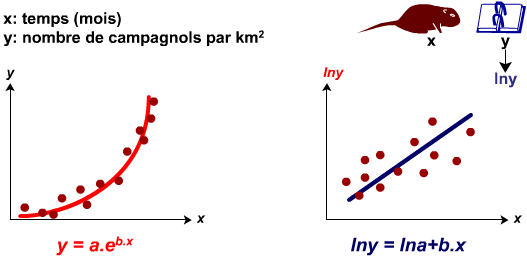
Modèle exponentiel: TeX Embedding failed!
Le modèle exponentiel se linéarise en calculant le logarithme népérien de y.
Exemple : Analyse de la croissance du nombre de campagnols par km carré en fonction du temps.
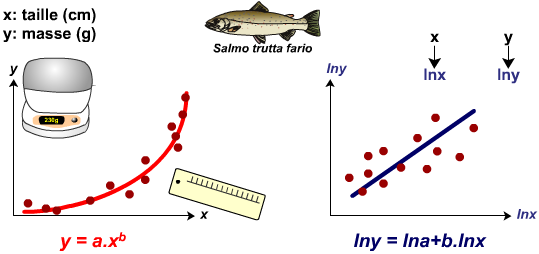
Modèle puissance: TeX Embedding failed!
Le modèle puissance se linéarise en calculant les logarithmes népériens de x et y.
Exemple : étude de la relation entre la taille et la masse de truites Farios.
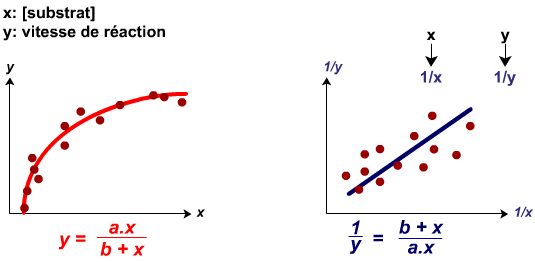
Modèle double inverse: TeX Embedding failed!
Le modèle double inverse se linéarise en calculant les inverses de x et y : TeX Embedding failed! et TeX Embedding failed!.
Exemple : analyse de la relation entre la concentration en substrat et la vitesse de réaction d'une enzyme.
Récapitulatif
Ce qu'il faut en retenir:
Lorsque l'animation commence, les points sont alignés horizontalement. Si à partir de cette situation rectiligne vous effectuez une rotation du nuage de points, le r et le R² prennent une valeur de 1 (ou -1 pour le r selon le sens de rotation), car les points restent parfaitement alignés, et que la pente est non nulle.
En modifiant individuellement la position des points, on peut constater que le r et le R² dépendent aussi bien de l'inclinaison du nuage de points que du rapprochement des points avec la droite de régression.
En déplaçant horizontalement ou verticalement ce nuage de points, le r et le R² ne sont pas modifiés, car ils tiennent compte des écarts entre les points (via la SPE), et non des valeurs absolues des coordonnées (X;Y).
Ce qu'il faut en retenir
Dans ce modèle, le R² n'est plus le carré du r et ces deux paramètres n'évoluent plus forcément de manière parallèle. Le r est dépendant de l'inclinaison du nuage, et le R² de la capacité de l'équation de régression à déterminer la distribution des points.
Note: Une notion non vue au cours (et donc non matière d'examen) est le leverage, que vous pouvez afficher en cliquant sur la petite case dans le coin inférieur droit. Le leverage mesure l’influence potentielle d’un point sur la droite. Il est calculé pour chaque point à partir des valeurs de X seulement, selon la formule: TeX Embedding failed!. Pour chaque point, le leverage varie de TeX Embedding failed! à 1. Les points très éloignés de la moyenne ont un plus grand leverage: ils ont plus de poids sur la détermination des paramètres a et b de la régression que ceux qui sont proches de la moyenne. Dans l'animation, les cercles bleus ont un rayon proportionnel à 2000 fois la valeur de leur leverage, afin de les rendre visibles. Vous remarquerez que lorsqu'il y a deux points (le nombre de points peut se modifier dans le petit cadre: on peut faire afficher de 2 à 9 points), les deux leverages sont égaux. Pour bien saisir le mode de variation d'un leverage, nous vous conseillons une simulation à 3 points.